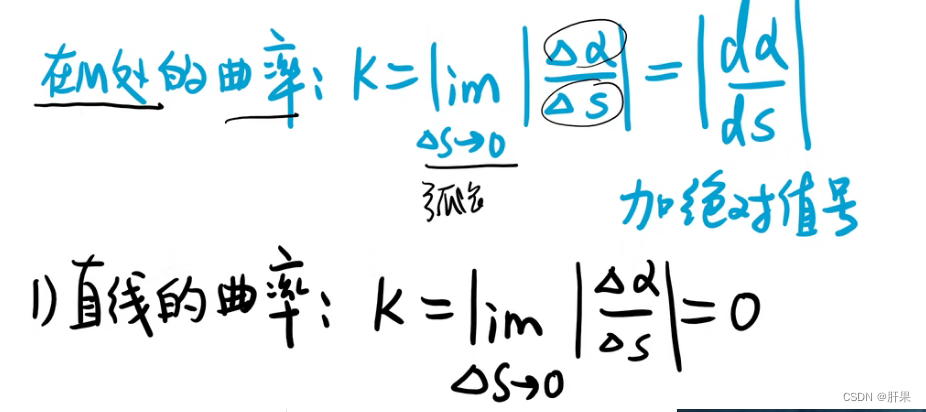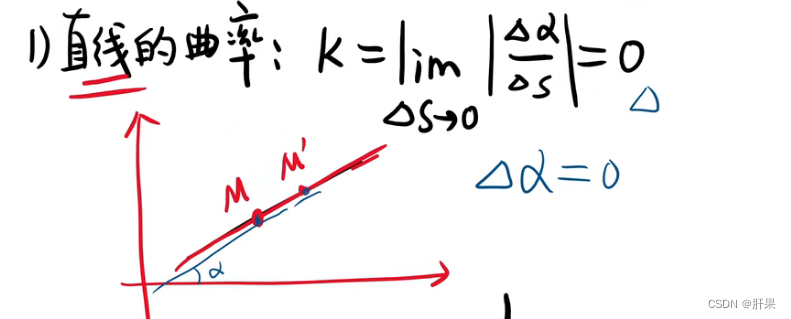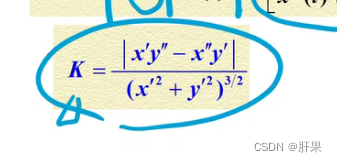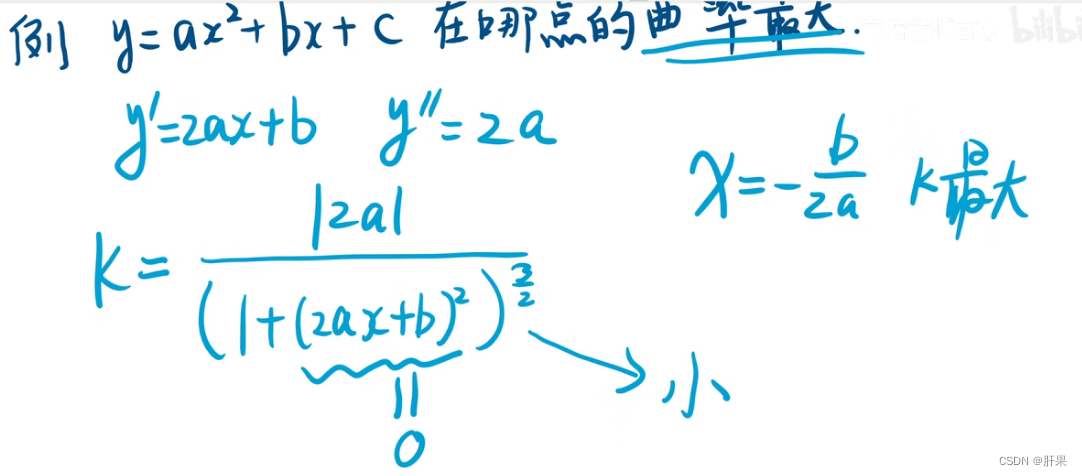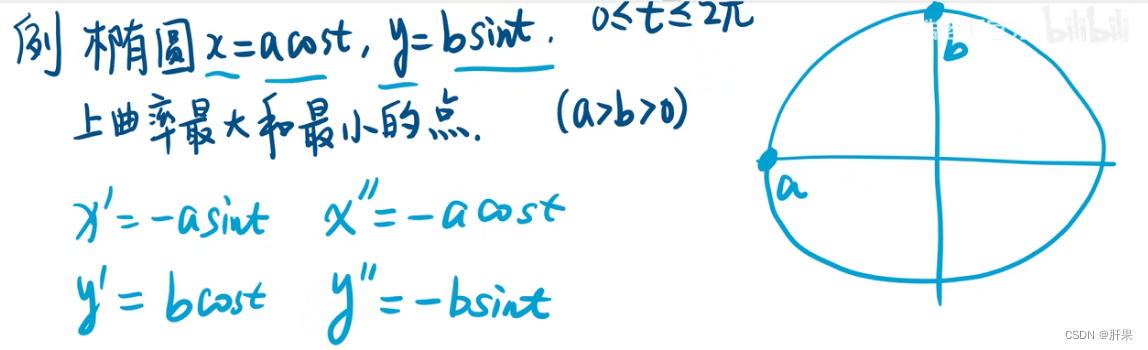厦门建设局怎么进宁波seo自然优化技术
微分的定义

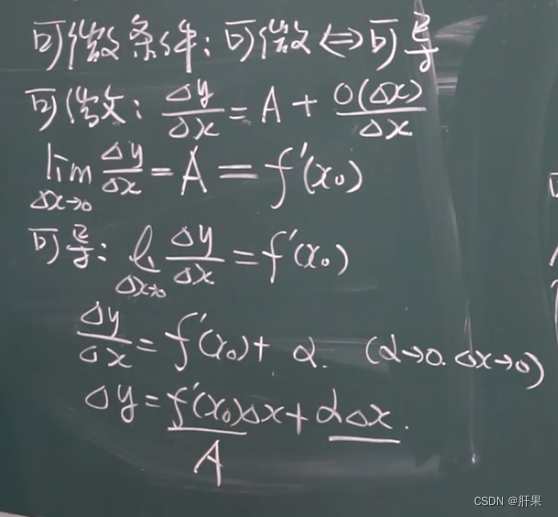
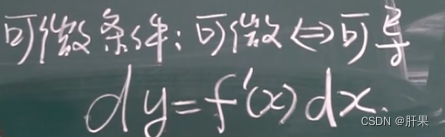
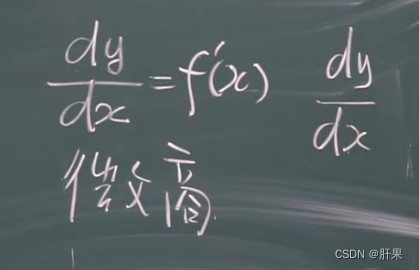
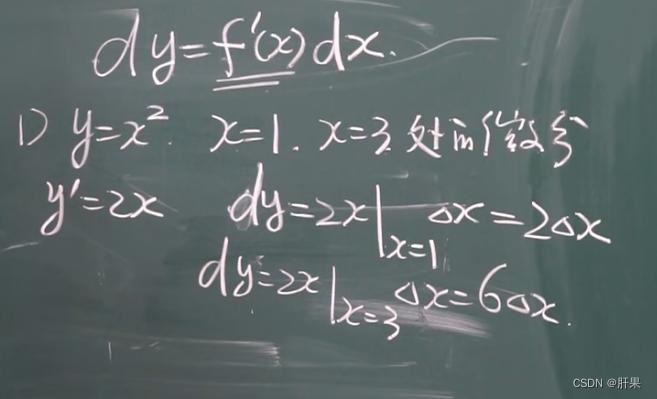
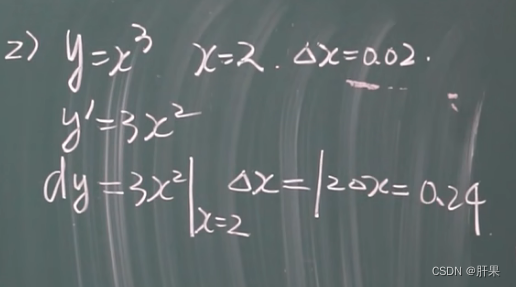
基本微分公式与法则
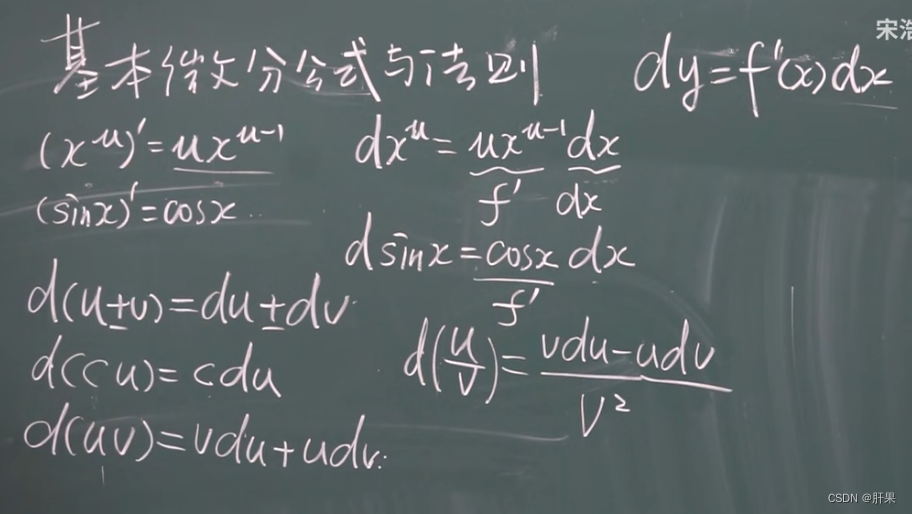
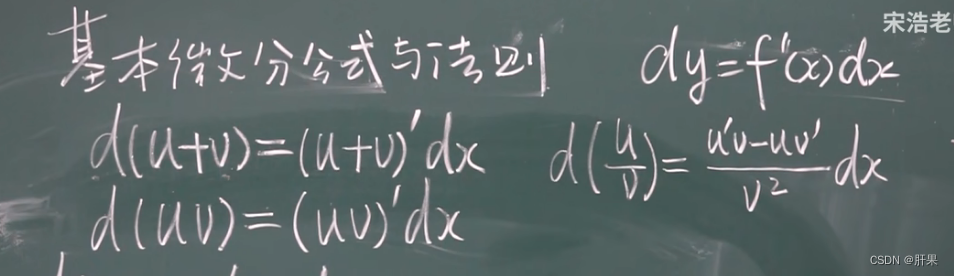
复合函数的微分
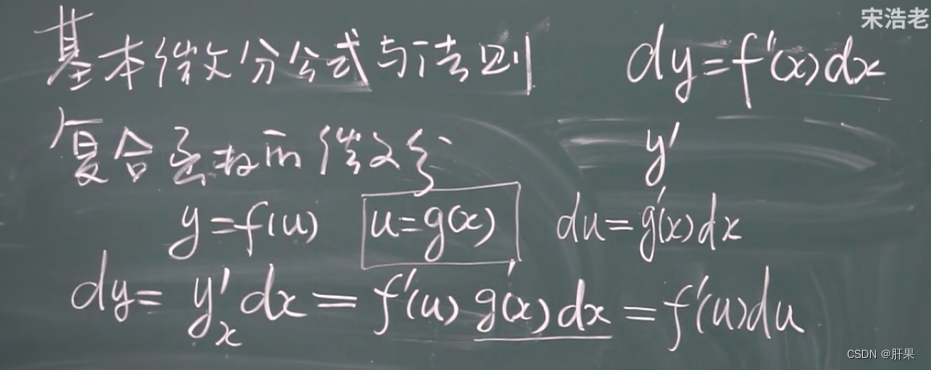
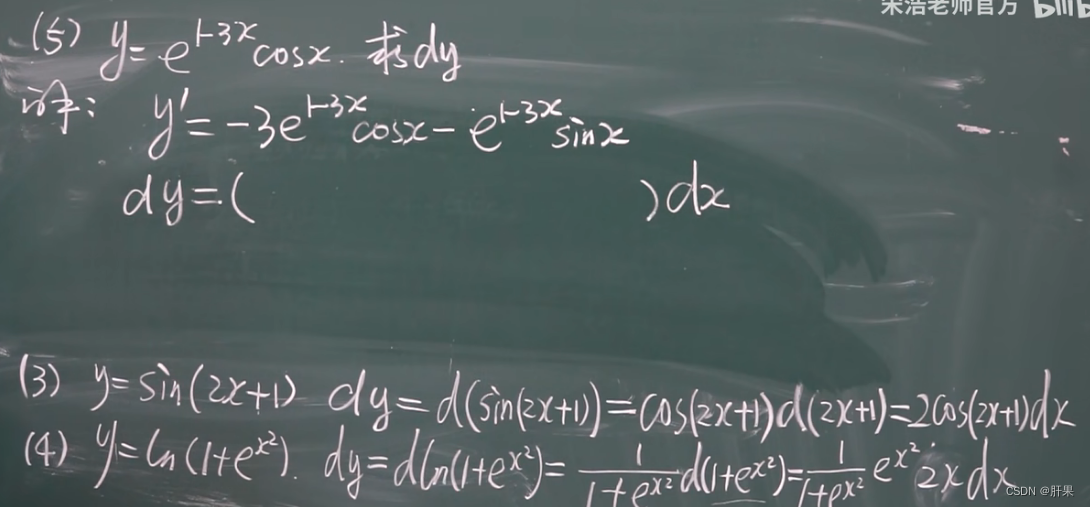
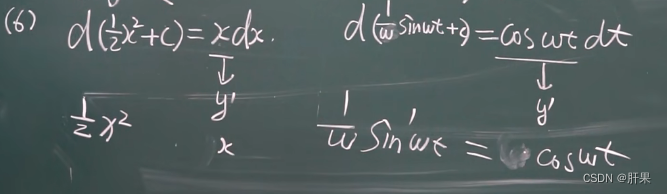
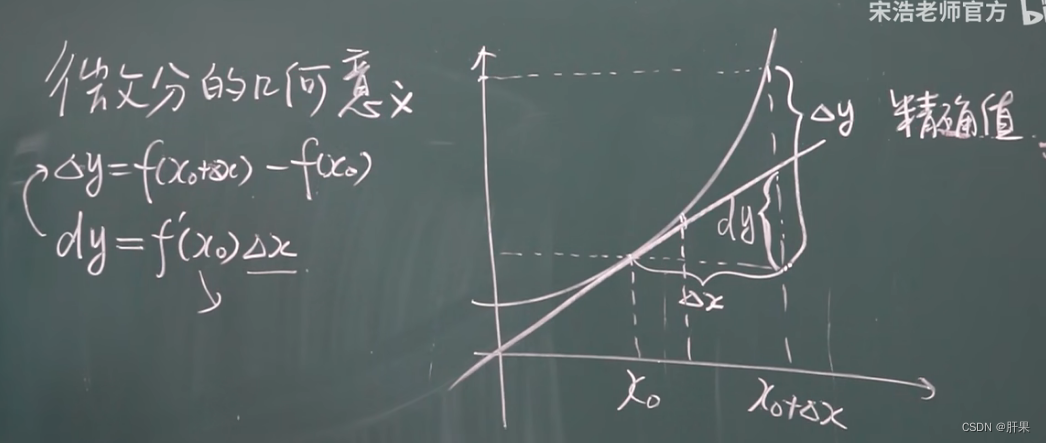
微分的几何意义
微分在近似计算中应用
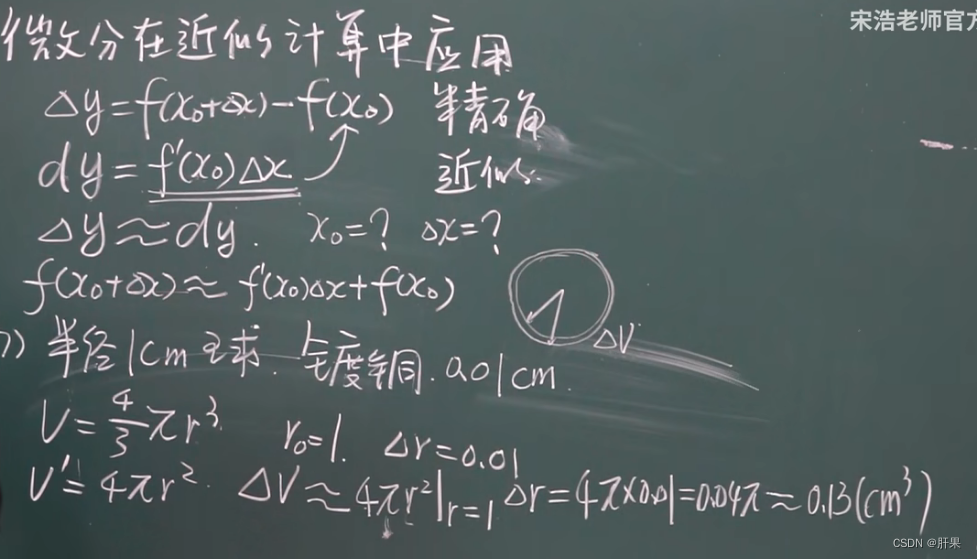

sin(x+y) = sin(x)cos(y) + cos(x)sin(y)可以用三角形的几何图形来进行证明。
假设在一个单位圆上,点A(x,y)的坐标为(x,y),点B(x’, y’)的坐标为(x’, y’)。则以两点为直角的直角三角形的斜边长为1,且所在的角为夹角x+y。
接下来,通过计算三角形中的各条边可以得到:
sin(x+y) = y’+y
cos(x+y) = x’+x
将cos x = x, sin x = y, cos y = x’ 和 sin y = y’ 代入上述公式得到:
sin(x+y) = sin(x)cos(y) + cos(x)sin(y)
至此,公式的正确性得到证明。
同时,我们还可以在单位圆上仿照上面的方法证明和差化积公式的正确性,这同样也是基于三角形的几何形式得到的。

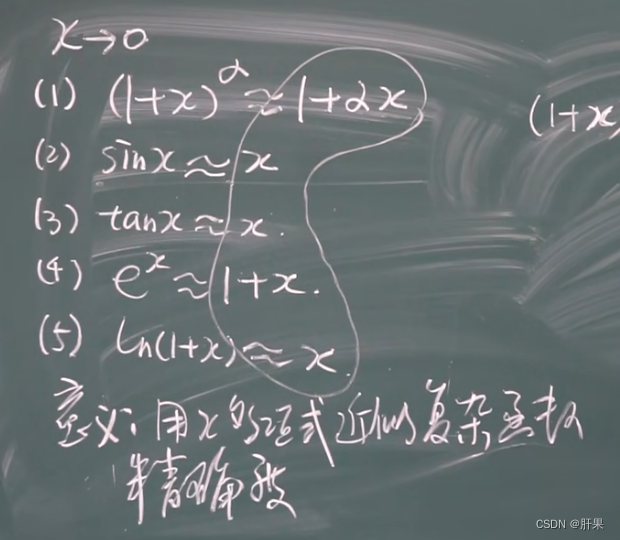
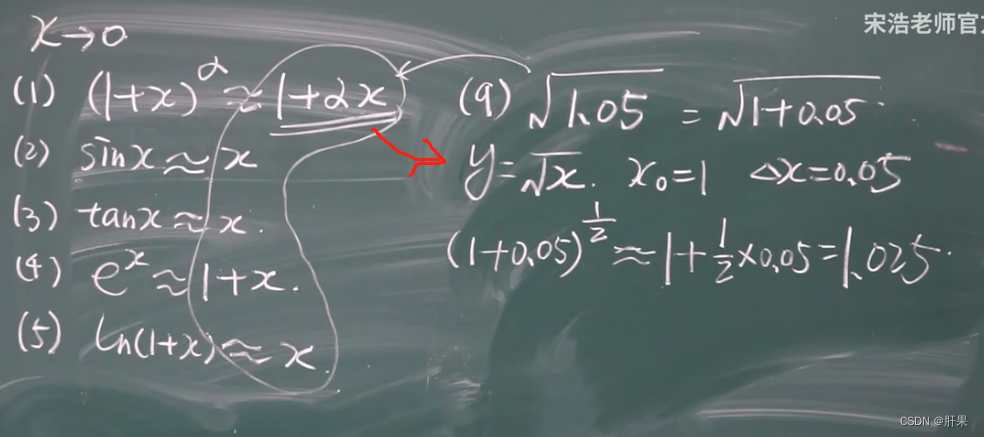
微分中值定理 罗尔定理




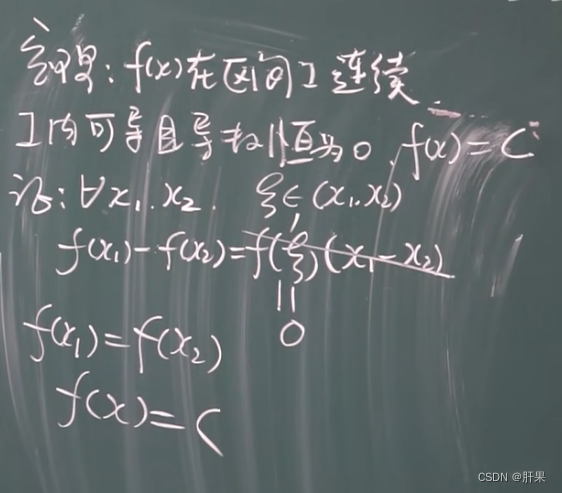
微积分中解决实际问题的过程一般包括两个步骤:微分和积分。
微分就是求导数,其本质是研究函数在某个点附近的局部变化,是一种用来描述函数变化情况的方法。而导数的定义是函数在某点处的变化速率,可以通过极限的方式准确地求解,不需要使用任何近似值。因此,导数的求解不需要近似值。
而微分的目的是为了研究函数在某个区间内的整体变化情况,例如函数的极值、拐点等。微分中经常需要计算函数的斜率,也就是导数。在一些情况下,我们无法直接求解导数,需要利用差商进行近似计算。这里的差商是指函数在两个点处的函数值之差与这两个点之间的距离之比,因此差商实际上是一种近似的导数计算方法。因此,微分中的近似计算需要使用差商这种近似的方法来实现。
另外,导数能够准确地描述函数在某点附近的局部变化,而微分则研究函数在整个区间内的整体变化情况。因此,在求解导数时,只需要关注函数在某点的变化情况,精度较高;而在微分过程中,则需要考虑整个区间内的变化情况,需要使用近似方法来近似计算。
柯西中值定理

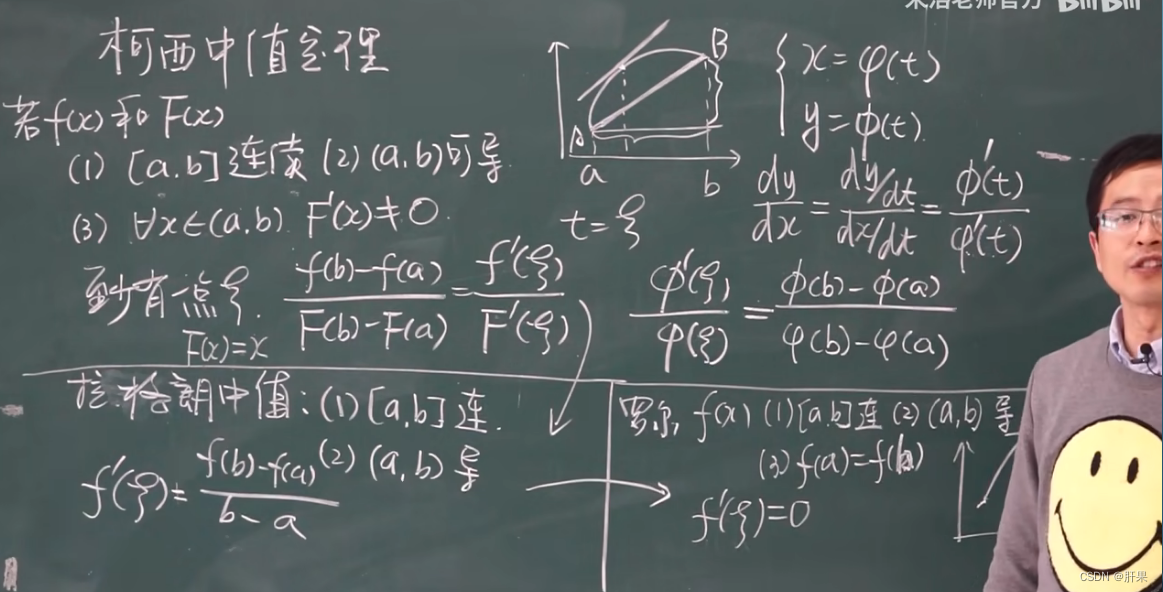
洛必达法则★★★★★
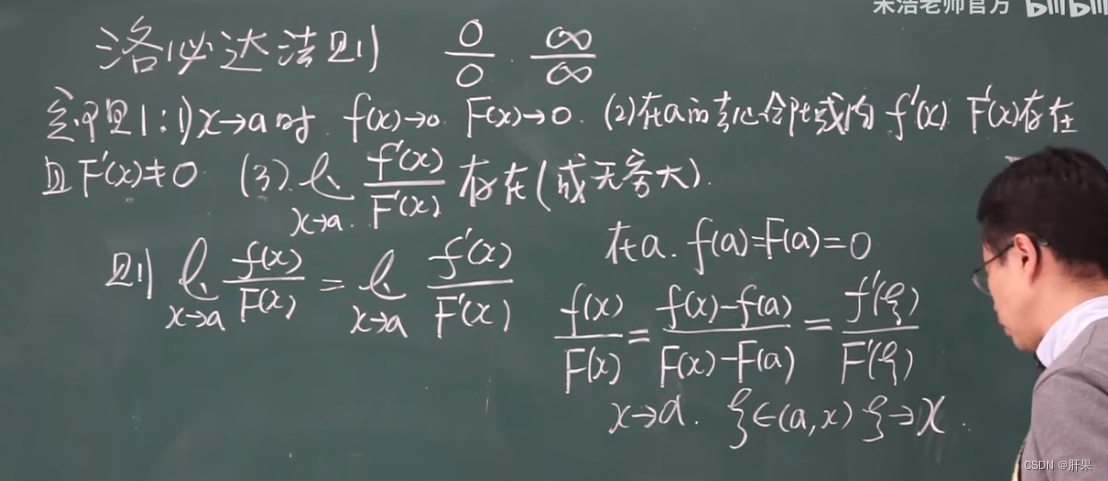

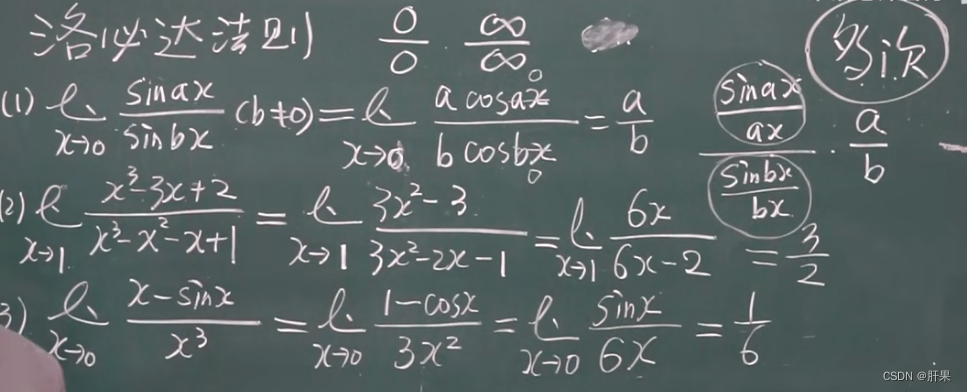


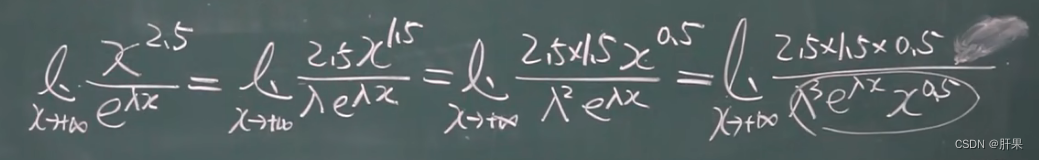
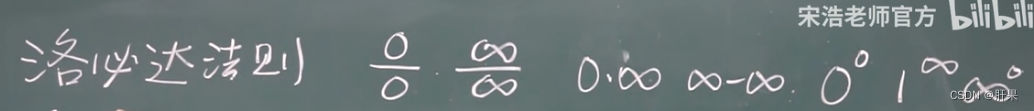
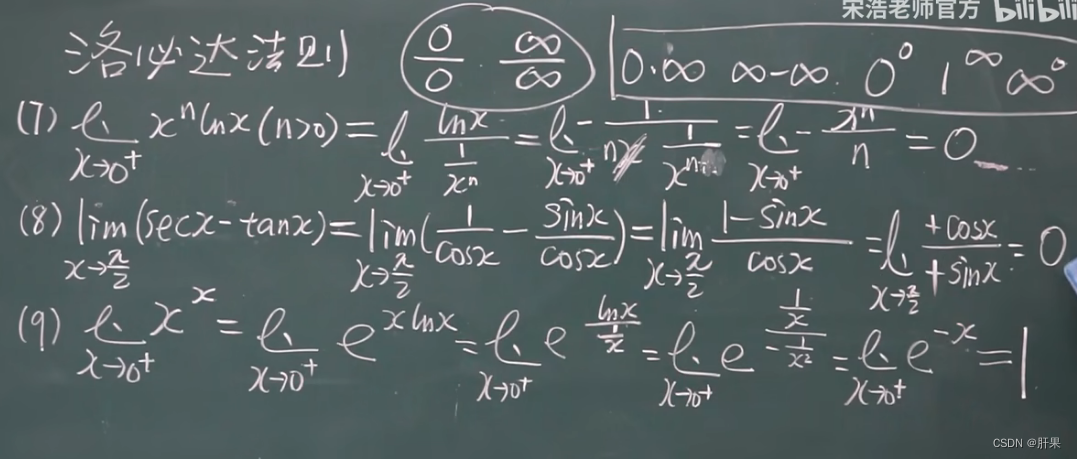

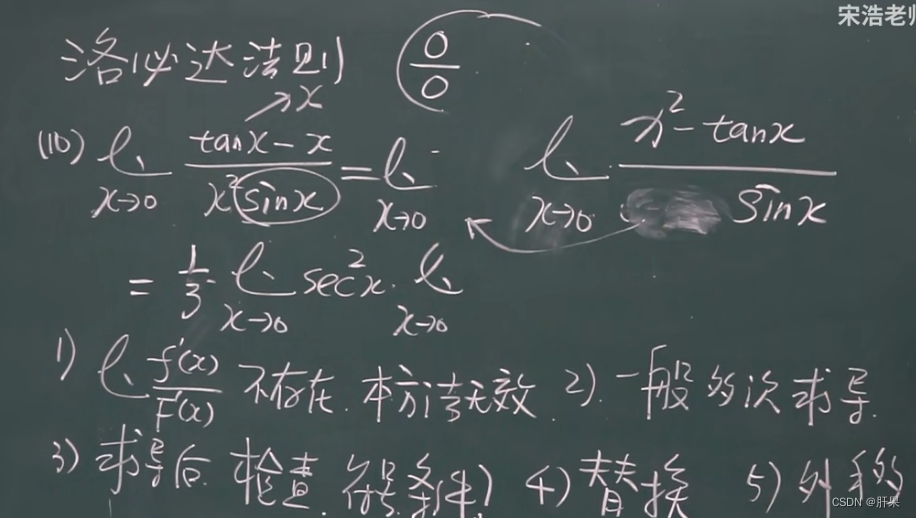
泰勒公式
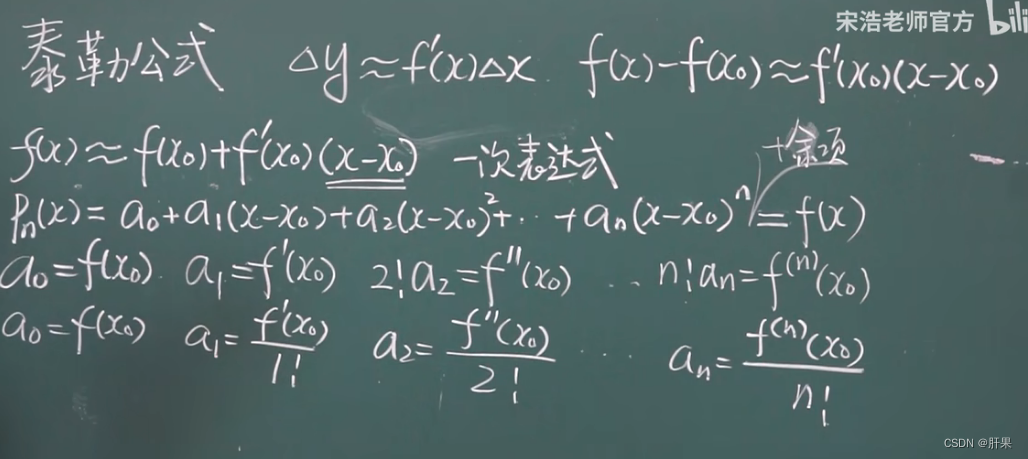
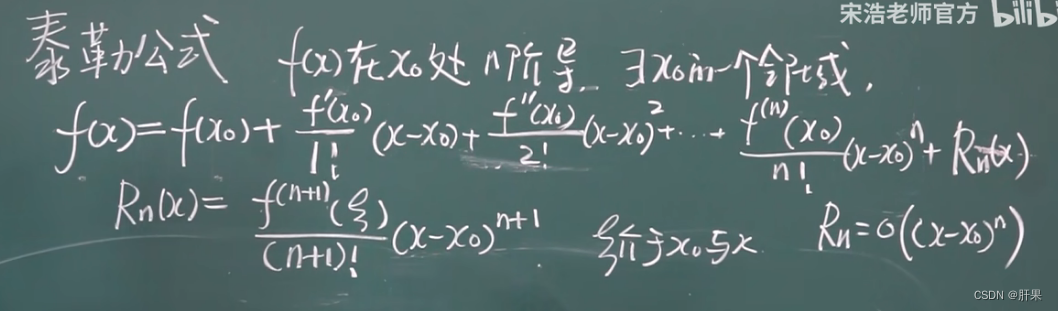

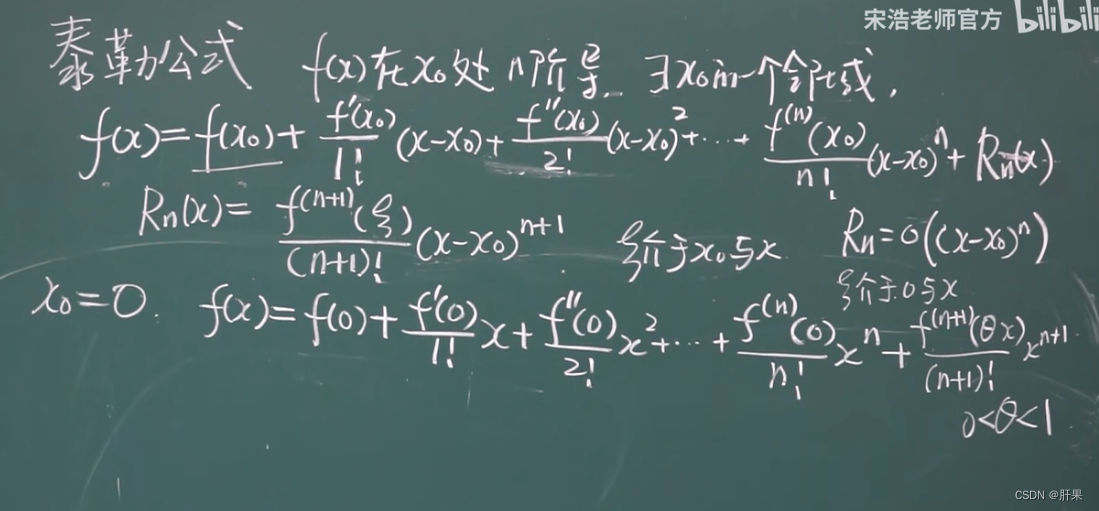
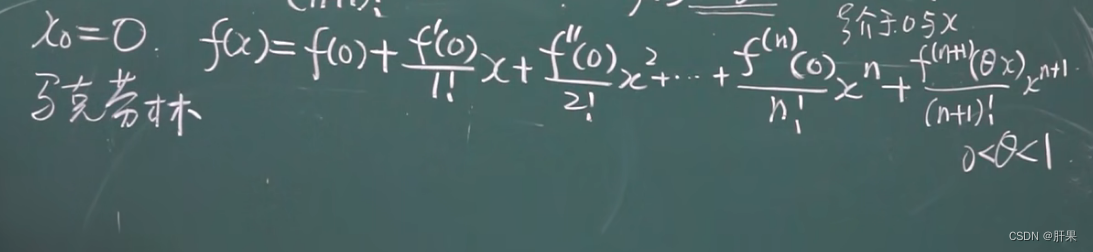


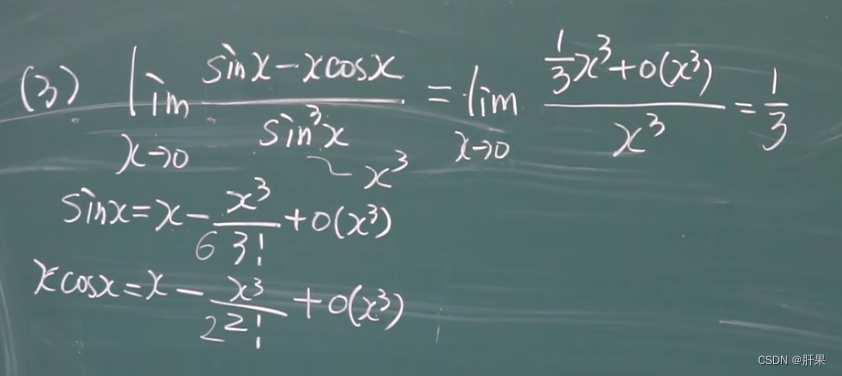
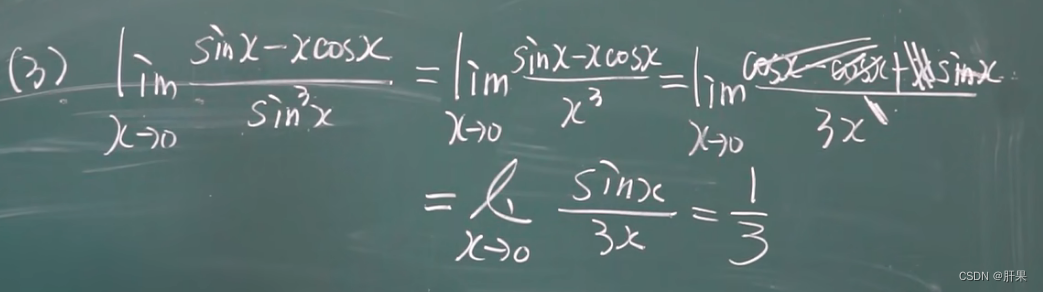
单调性


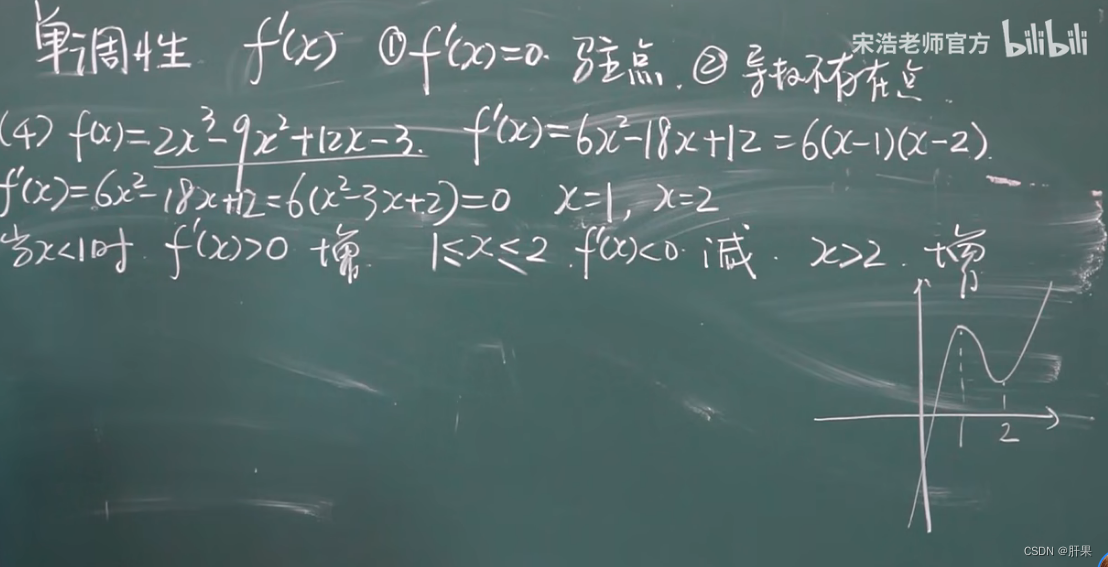

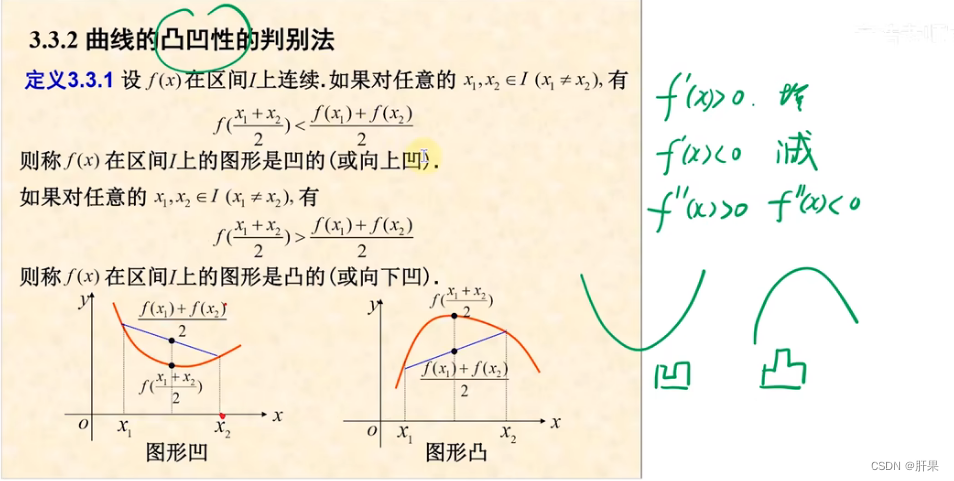






极值与其求法
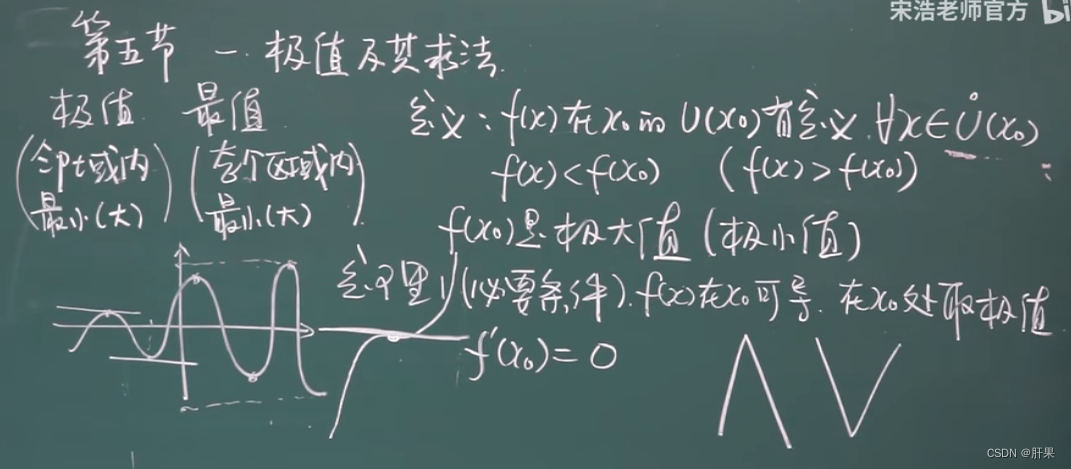
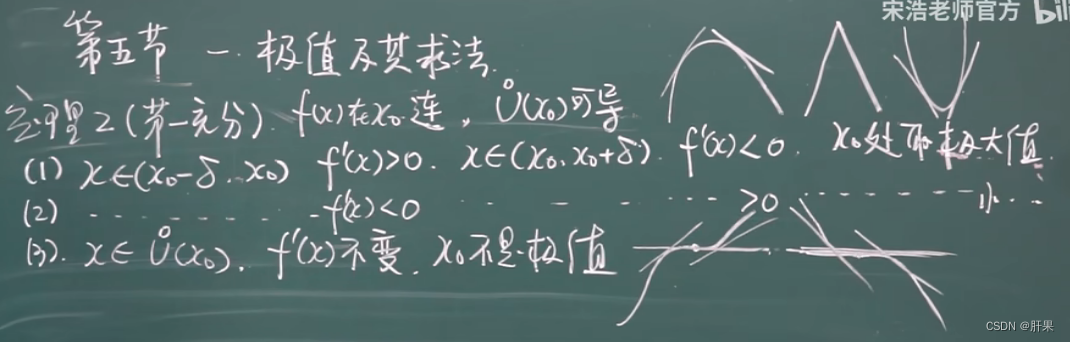



渐近线
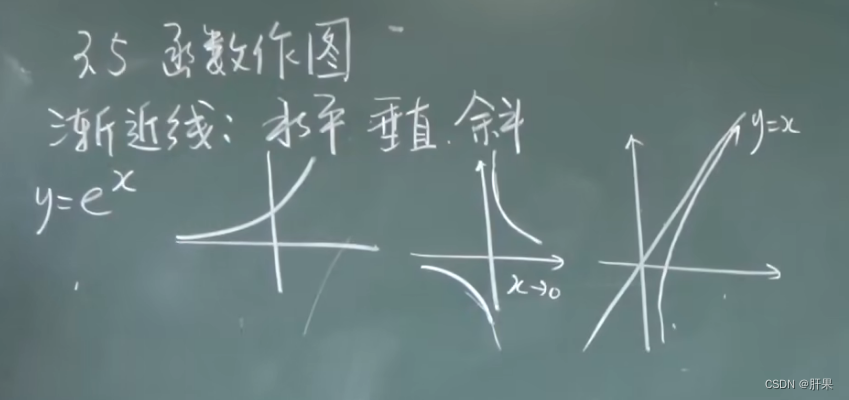
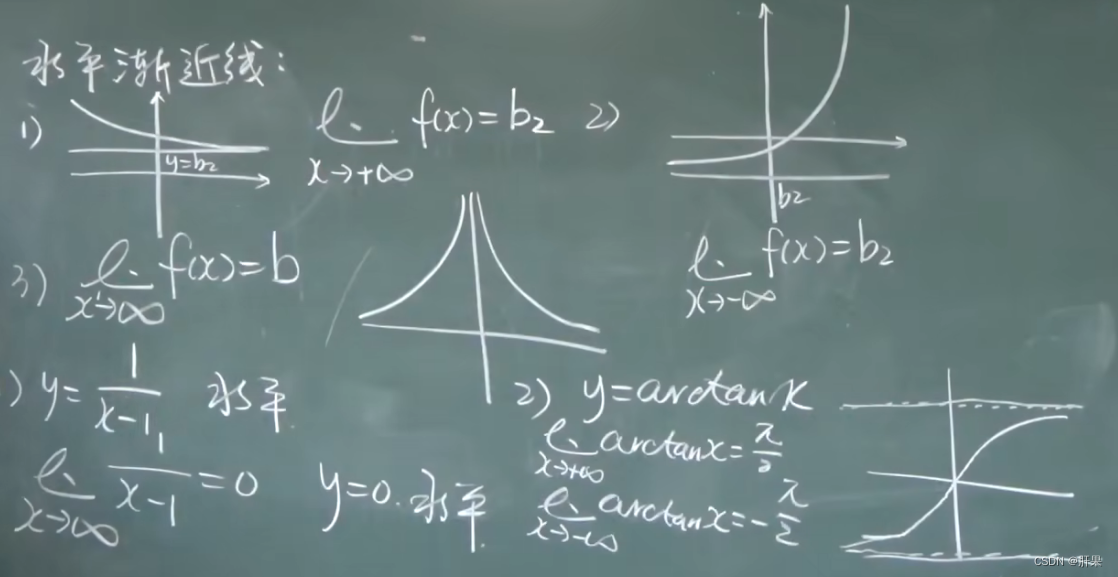
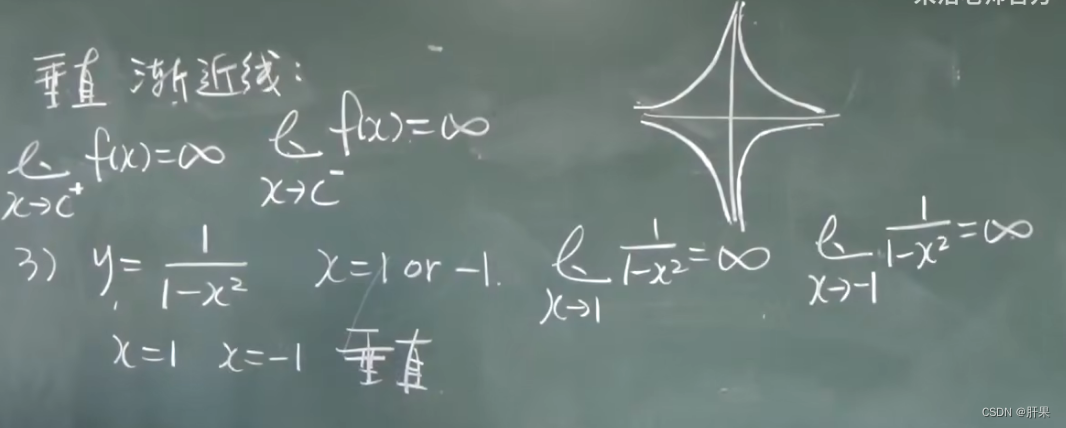
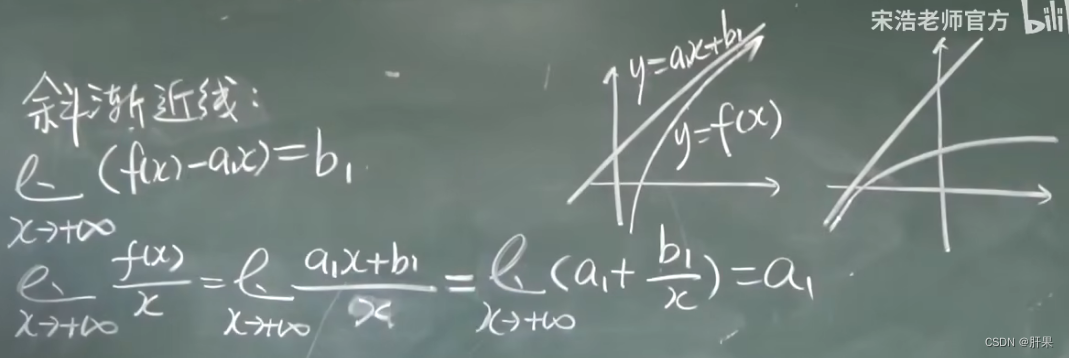
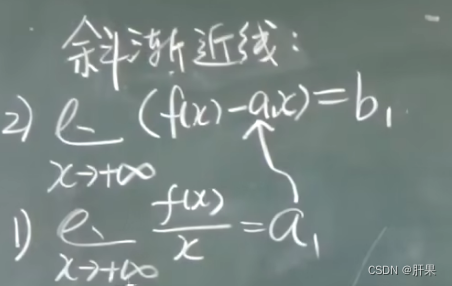
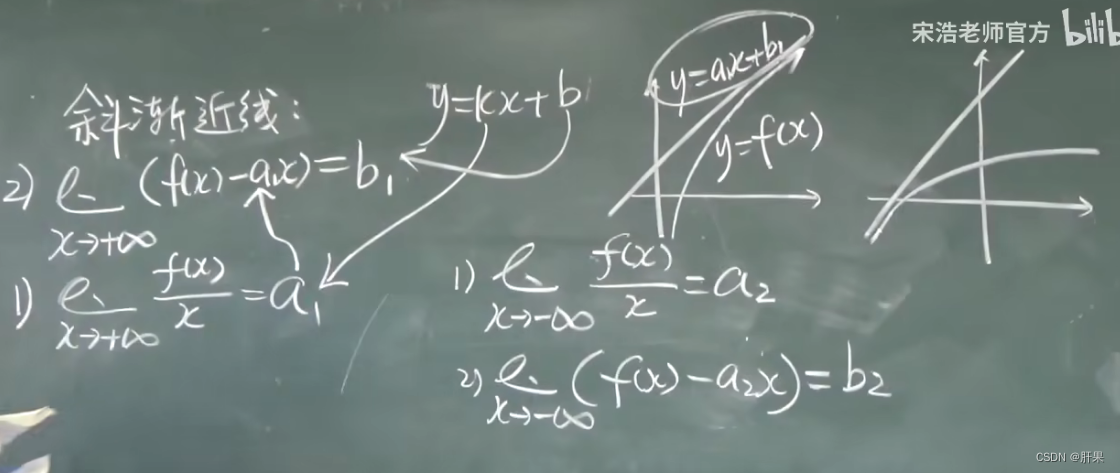
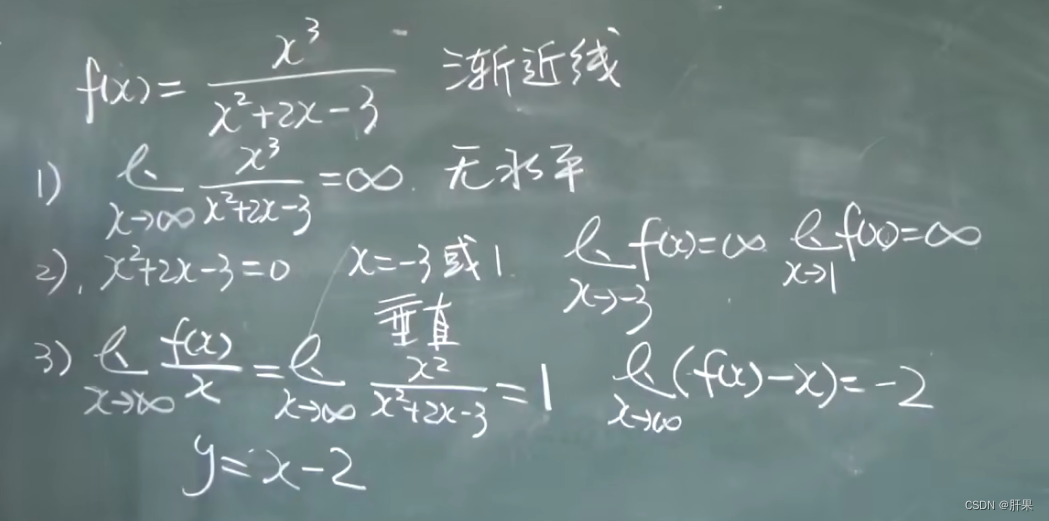
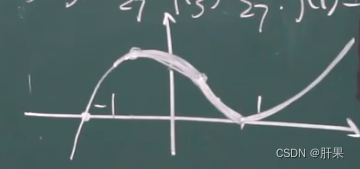
函数图形的绘制

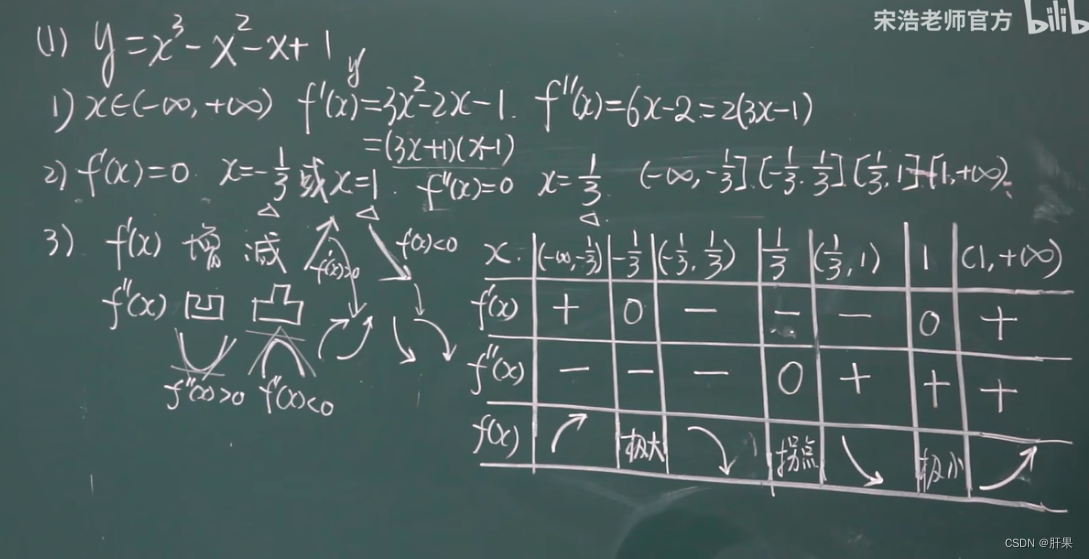
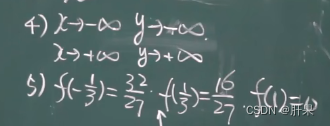
为什么偶函数求导就是奇函数?
设 f(x) 是一个偶函数,即 f(x) = f(-x)。则有:
f’(x) = lim(h→0)[f(x+h) - f(x)]/h
将 h 替换为 -h,得到:
f’(-x) = lim(-h→0)[f(-x+h) - f(-x)]/h
因为 f(x) 是偶函数,所以 f(-x+h) = f(-(x-h)) = f(x-h),且 f(-x) = f(x),可以得到:
f’(-x) = lim(h→0)[-f(x-h) + f(x)]/(-h)
因为减去一个数可以看作加上它的相反数,即 -f(x-h) = f(-(x-h)) = f(x+h),可以得到:
f’(-x) = lim(h→0)[f(x+h) - f(x)]/h = f’(x)
所以 f(x) 的导函数 f’(x) 是偶函数。
因此,若偶函数 f(x) 求导后得到的导函数为 f’(x),则 f’(x) 是奇函数。


这是二次方程标准形式,可以使用求根公式(也称为“二次公式”)求解。
二次公式:
对于二次方程 ax^2 + bx + c = 0,解的公式为:
x = (-b ± √(b^2 - 4ac)) / 2a
即,解为两个根:
x1 = (-b + √(b^2 - 4ac)) / 2a
x2 = (-b - √(b^2 - 4ac)) / 2a
其中±表示两种可能的符号(+或-),√表示算术平方根。
根的性质:
-
当 b^2 - 4ac > 0 时,方程有两个不相等的实数根。
-
当 b^2 - 4ac = 0 时,方程有两个相等的实数根。
-
当 b^2 - 4ac < 0 时,方程没有实数根,但有两个共轭复根。
注意:
求根公式对于系数 a 不为 0 的二次方程适用,对于 a = 0 的情况,此时方程不再是二次方程,而是一次方程。
另外,在实际计算过程中,要注意避免出现计算误差或溢出等情况,需要采取适当的数值稳定性措施。

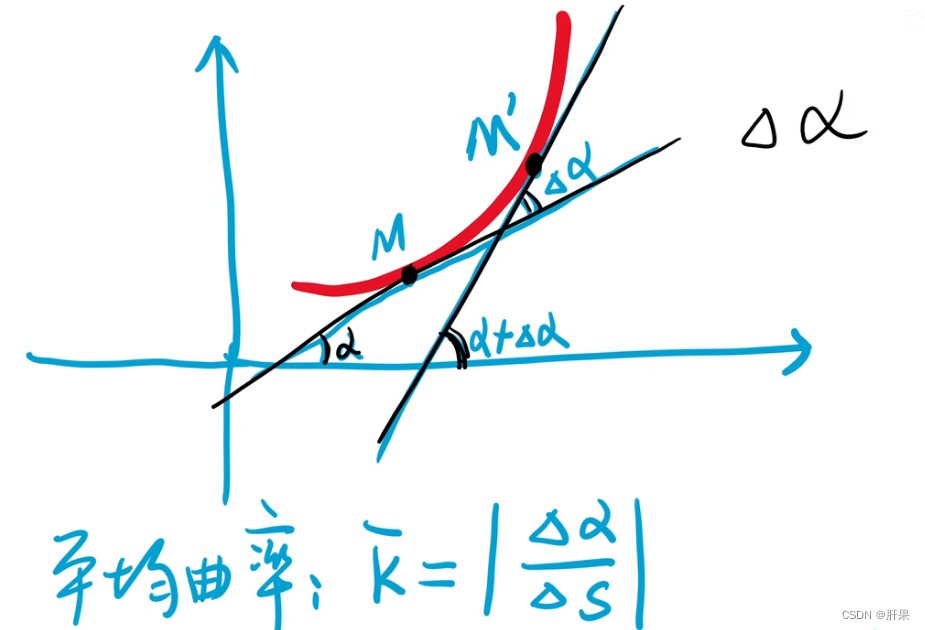
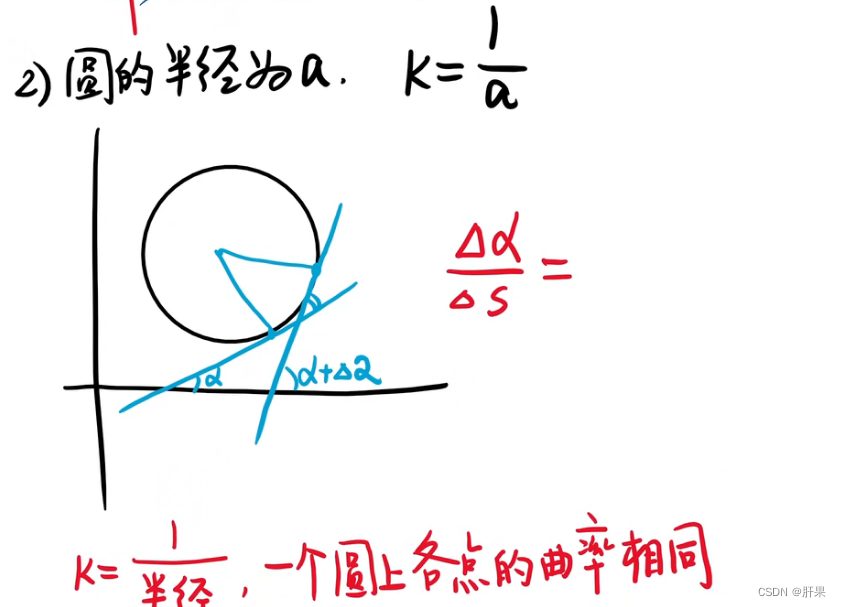
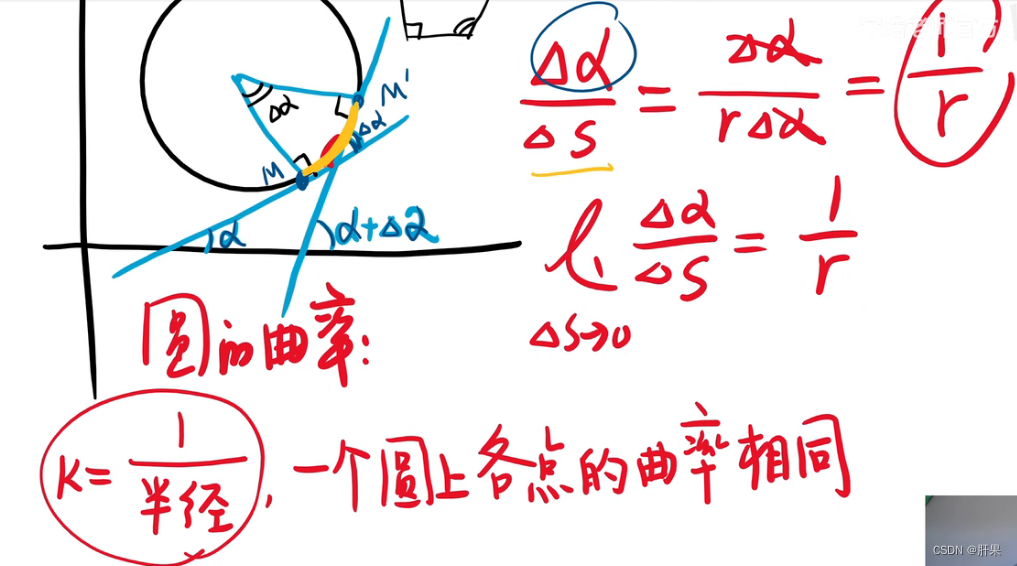
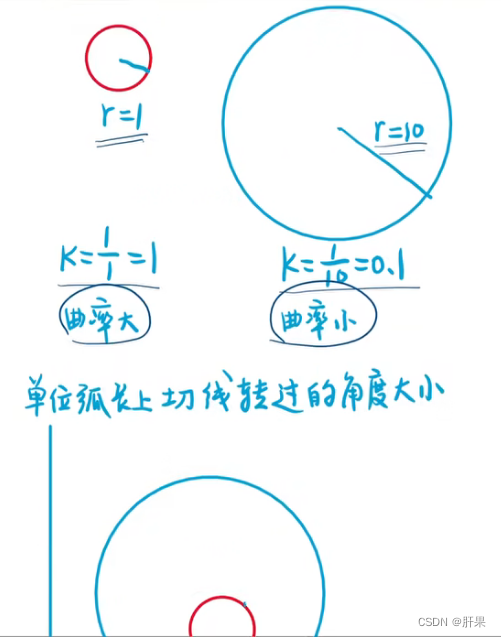
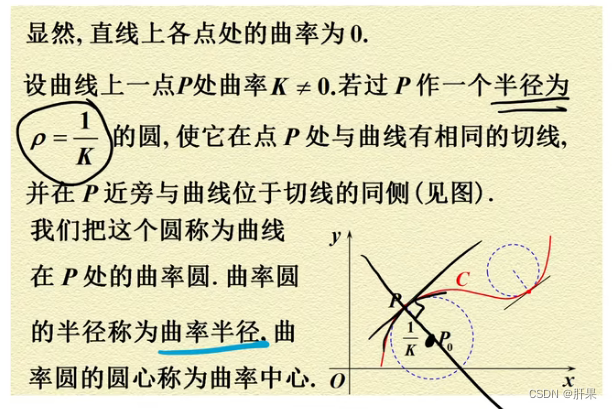
曲率