深圳市移动端网站建设全部视频支持代表手机浏览器
本文主要讲解的是c语言函数递归的知识点
目录
基础概念
什么是递归?
递归的条件
递归的优点和缺点
举例
1、死循环
2、n的阶乘
3、求n的k次方
4、打印一个数的每一位
应用
斐波那契数列
青蛙跳台问题
汉诺塔问题
基础概念
什么是递归?
递归是一种算法或函数调用自身的过程。在递归过程中,问题被分解为规模更小的同类问题的子问题,直到达到终止条件。
简单来讲,递归就是递推回归,函数自己调用自己的过程就是递归。
递归的条件
1. 将问题转化为其子问题,子问题要与原问题具有相同的解法。
递归存在限制条件,当满足这个限制条件的时候,递归便不在继续。
2. 递归的出口,每次递归调用之后越来越接近这个限制条件。
递归的优点和缺点
优点:
- 递归能够简化问题的解决过程,使代码更加简洁和易读。
- 递归能够将复杂的问题分解为更小的子问题,从而降低问题的复杂度。
- 递归能够提供一种优雅的解决方案,特别是对于某些问题,递归的思想更加自然和直观。
缺点:
- 递归可能导致性能问题,特别是在处理大规模问题时。递归的函数调用会占用额外的内存空间,并且可能导致栈溢出。
- 递归可能导致代码的执行效率较低,特别是在处理重复计算的情况下。递归的函数调用可能会重复执行相同的计算步骤。
- 递归可能导致代码的理解和调试变得困难。递归的执行过程比较隐式,可能需要更多的思考和调试工作。
我们知道,在c语言每一次函数调用,都需要为本次函数调用在栈区申请空间来保存函数调用期间的各种局部变量的值,这块空间称为运行时堆栈,或者函数栈帧。
若函数不返回,函数对应的栈帧空间就会一直占用,所以当采用函数递归来完成代码,当递归太深时,就会浪费太多的栈帧空间,可能会导致栈溢出(Stack overflow)。
具体的代码会在下面举例中详细解答。
举例
1、死循环
我们知道main()函数也是一个函数,所以我们也可以在main()函数中调用它自己。
#include<stdio.h>int main()
{printf("hhhhh\n");main();return 0;
}当我们调试时,我们会遇到这种情况:
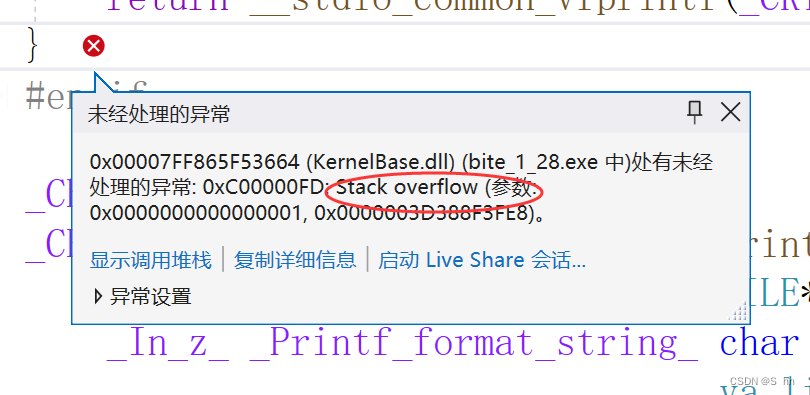
这就是我们上面提到的栈溢出问题。
如何去理解呢?
我们知道,每一次函数调用,都会在栈区里面上申请一块空间。
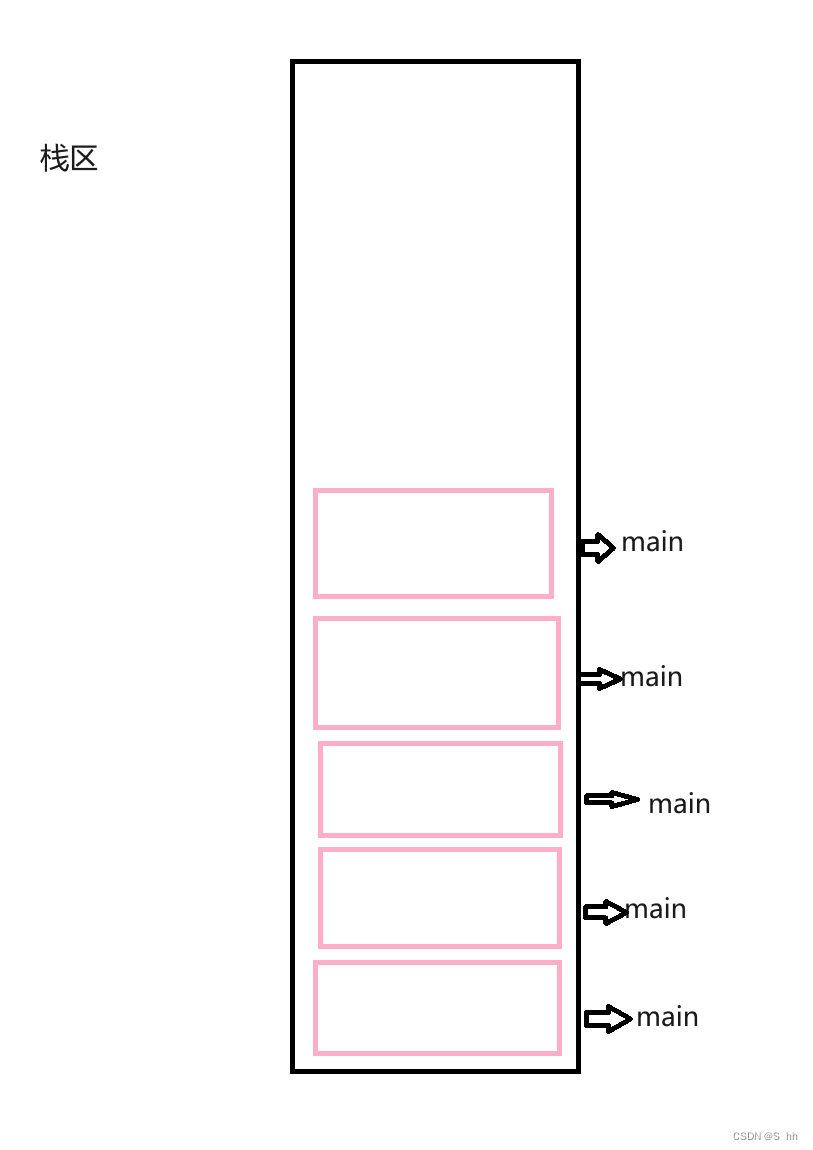
以上代码会产生死循环,也就是说它会一直申请栈帧空间,但并不会释放,而栈区空间并不是无限大,因此会产生栈溢出问题。
2、n的阶乘
一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶乘写作n!。
1!=1;
2!=1*2 = 2*1! ;
3!=1*2*3 = 3*2! ;
4!=1*2*3*4 = 4*3! ;
5!=1*2*3*4*5 = 5*4! ;
.
.
.
n!=1*2*3*4......n = n*(n-1)! ;
根据以上规律,我们可以写出代码:
int Fac(int n)
{if (n == 0)return 1;return n * Fac(n - 1);
}
3、求n的k次方
编写一个函数实现n的k次方,使用递归实现。
n的1次方:n
n的2次方:n*n =n*n的1次方
n的3次方:n*n*n =n*n的2次方
n的4次方:n*n*n*n =n*n的3次方
.
.
.
n的k次方: n*n*n......*n =n*n的k-1次方
推导出n的k次方的规律,可以写出代码:
int Pow(int n, int k)
{if(k==0)return 1;else if(k>=1){return n*Pow(n, k-1);}
}4、打印一个数的每一位
递归方式实现打印一个整数的每一位
思路:
N N <= 9 Print(N)=Print(N-1), 打印N
print(n)
print(n/10); printf("%d",n%10);
当我们给出一个数:1234
print(1234): print(123);printf("%d",1234%10);
|
|
print(12);printf("%d",123%10);
|
|
print(1);printf("%d",12%10);
|
|
print("%d",1%10);(1<9)
代码实现:
void print(unsigned int n){if(n>9)print(n/10);printf("%d ", n%10);}
应用
斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……。在数学上,斐波那契数列以如下被以递推的方法定义:F(1)=1, F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥3,n ∈ N*)。
思路:
1 N < 3 Fac(N) = Fac(N-1) + Fac(N-2) N >= 3
代码:
long long Fac(int N)
{if(N < 3)return 1;return Fac(N-1) + Fac(N-2);
}当我们使用递归的方法来解决这个问题时;
当n==12, 3 ,4 25 等可以很快的得出结果,但是当我们输入的n=50时,就会出现下面的情况:
并没有结果显示,那计算机到底有没有在计算呢?我们查看一下任务管理器会发现它确实在计算,只不过这个计算次数比较大。

那我们如果想要得到50甚至有大于50的斐波那契数列,怎么去优化?
1 1 2 3 5 8 13 21......
令a=1,b=1;
{
c=a+b;
a=b;
b=c;
}
依次类推,直至算到第n个数。
代码:
long long Fib(int n)
{long long a = 1, b = 1, c;int i = 3;while (i <= n){c = a + b;a = b;b = c;i++;}return b;
}int main()
{int n;scanf("%d", &n);long long t=Fib(n);printf("%lld", t);return 0;
}运行结果:

青蛙跳台问题
题目描述:
一只青蛙跳一次只能跳1级台阶或跳2级台阶。
求:该青蛙跳上第n级台阶总共有多少种跳法?
思路:
当只有一个台阶时:
青蛙只有一种跳法;
当有两个台阶时:
青蛙可以一次跳两个台阶,也可以先跳一个台阶,再跳一个台阶;
当有三个台阶时:
青蛙第一次有两种选择:1、跳一个台阶 2、跳两个台阶
当选择1时:青蛙还剩下两个台阶,当只有两个台阶时,我们已经得出是两种跳法;
当选择2时:青蛙还剩下一个台阶,当只有一个台阶时,我们已经得出是一种跳法;
所以三个台阶的跳法是:选择1+选择2=3;
当有四个台阶时:
青蛙第一次有两种选择:1、跳一个台阶 2、跳两个台阶
当选择1时:青蛙还剩下三个台阶,当有三个台阶时,我们已经得出是三种跳法;
当选择2时:青蛙还剩下两个台阶,当有两个台阶时,我们已经得出是两种跳法;
所以三个台阶的跳法是:选择1+选择2=5;
同理:
有n个台阶:
jump(n)=jump(n-1)+jump(n-2);
代码实现:
#include<stdio.h>int jump(int n)
{if (n == 1)return 1;if (n == 2)return 2;return jump(n - 1) + jump(n - 2);
}
int main()
{int n;scanf("%d", &n);int t=jump(n);printf("%d", t);
}汉诺塔问题
汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
思路:(下面内容是求移动需要的步骤,并不包含每一步的步骤)
当柱子上只有一个圆盘:这种情况只需要一步就可以将圆盘移动到第三根石柱上;
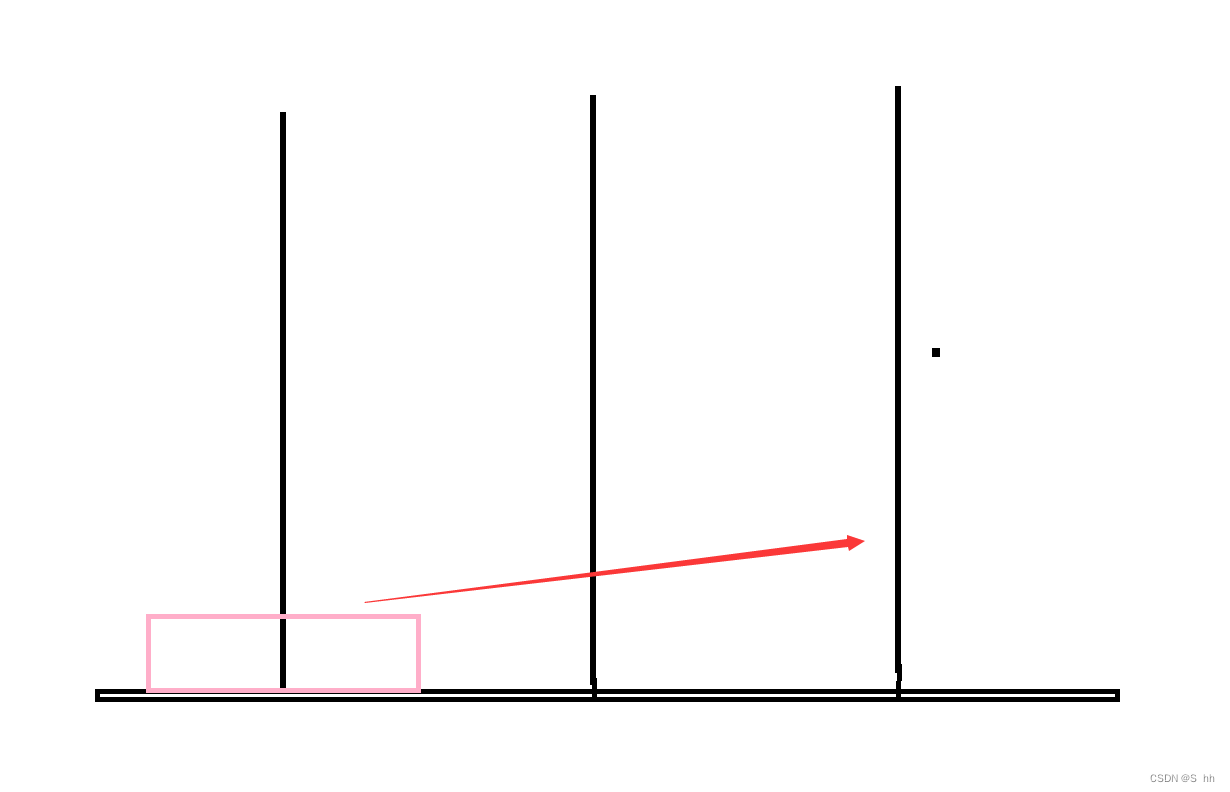
当柱子上有两个圆盘:这种情况需要三步来移动圆盘;
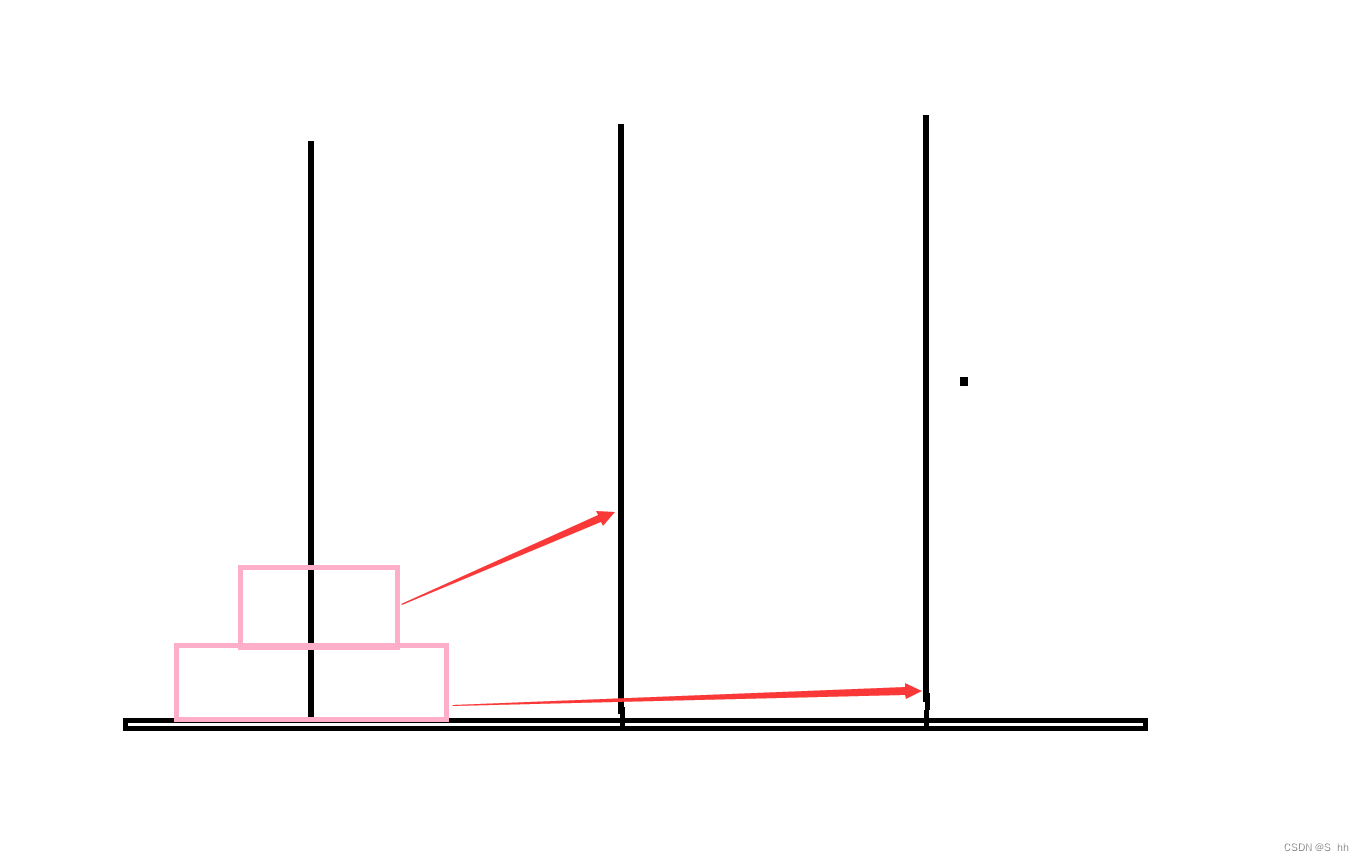
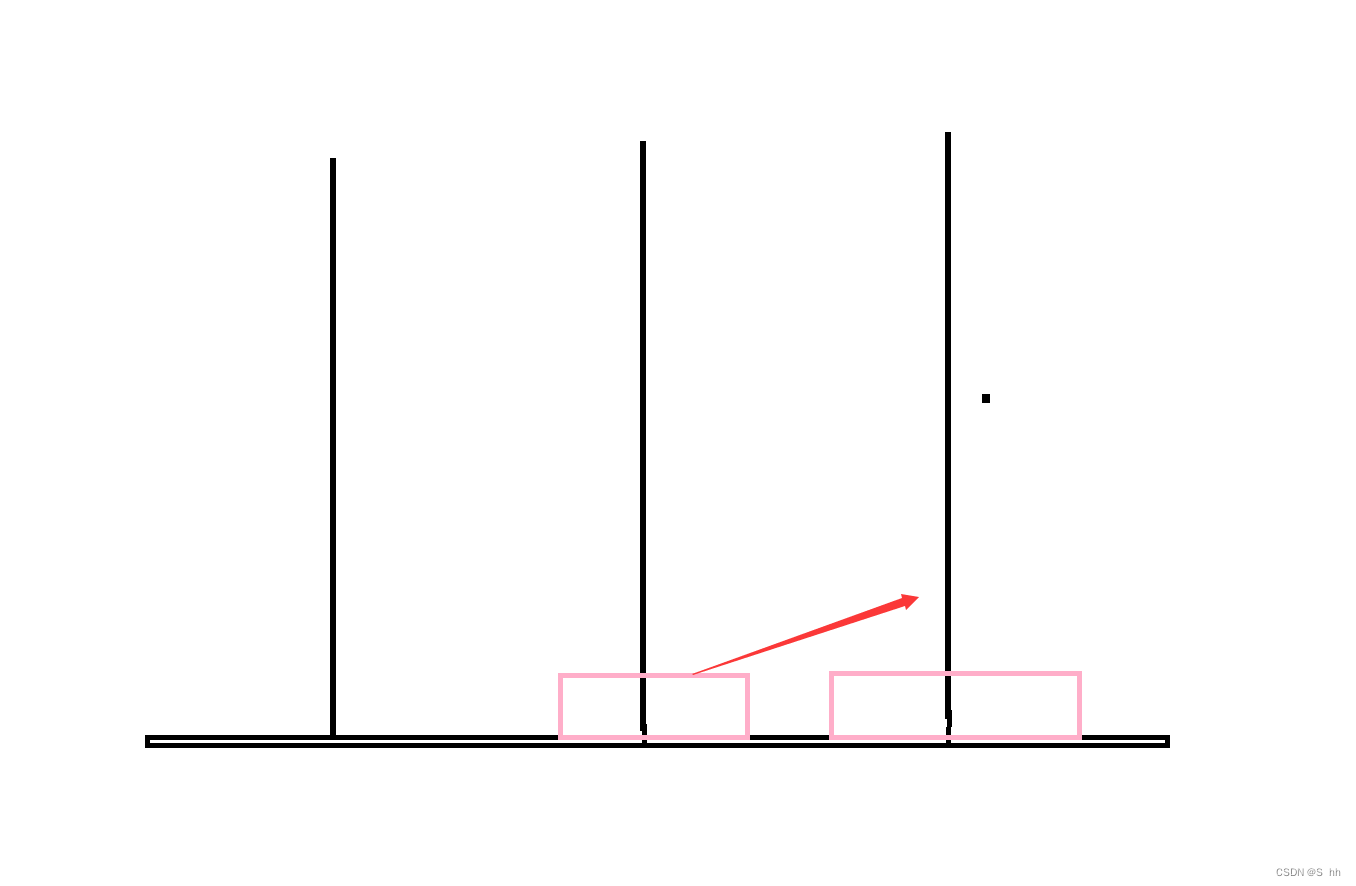
当柱子上有三个圆盘:
第一步:我们需要先将上面两个圆盘移动到第二根石柱
第二步:再将最后的石柱移动到第三根
其中第一步和当柱子上有两个圆盘类似,其步骤也是相同为3步;第二步和当柱子上只有一个圆盘类似,只需要1步。
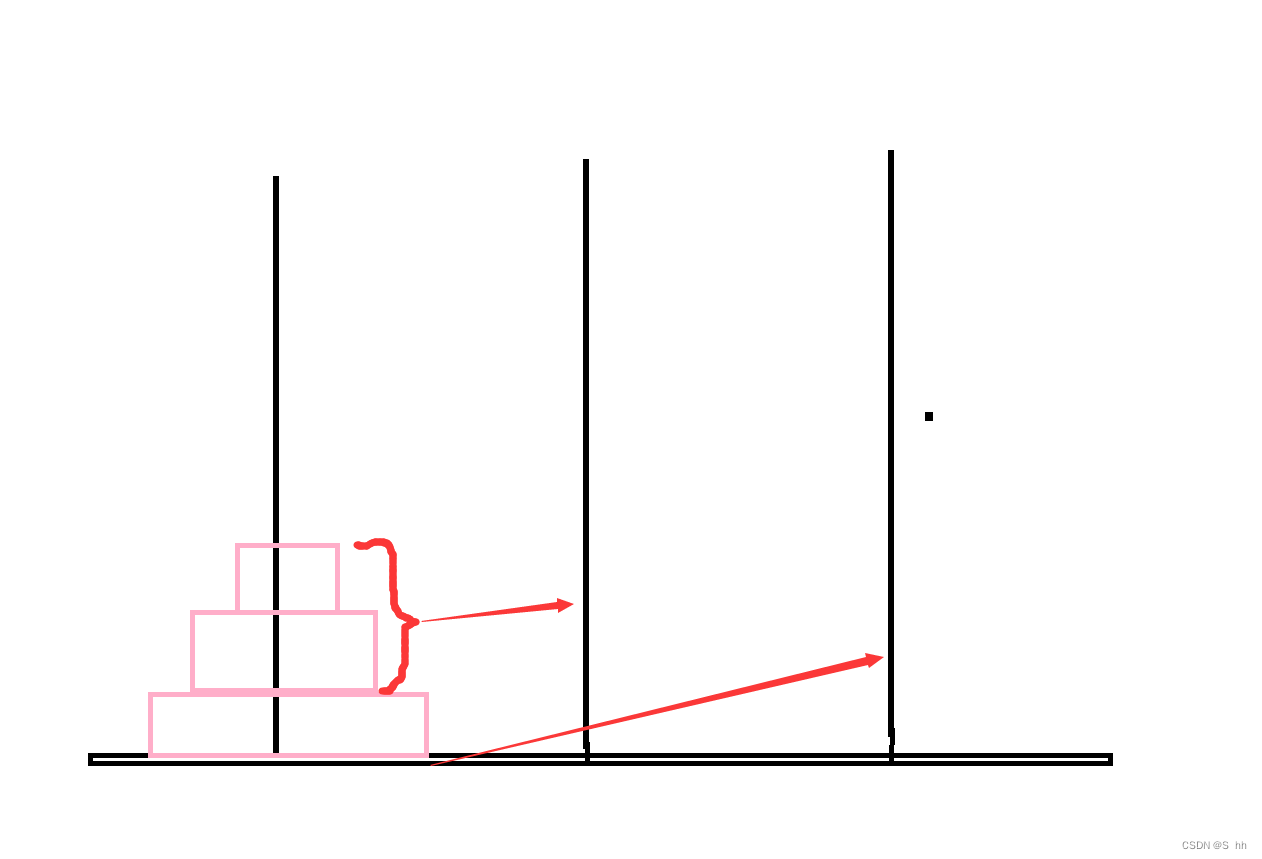
第三步:我们只需要将剩下的两个石柱移动到第三根上去,其步骤和当柱子上有两个圆盘类似,为3步;
综上,我们可以得出当柱子上有三个圆盘步骤:3+1+3=7;
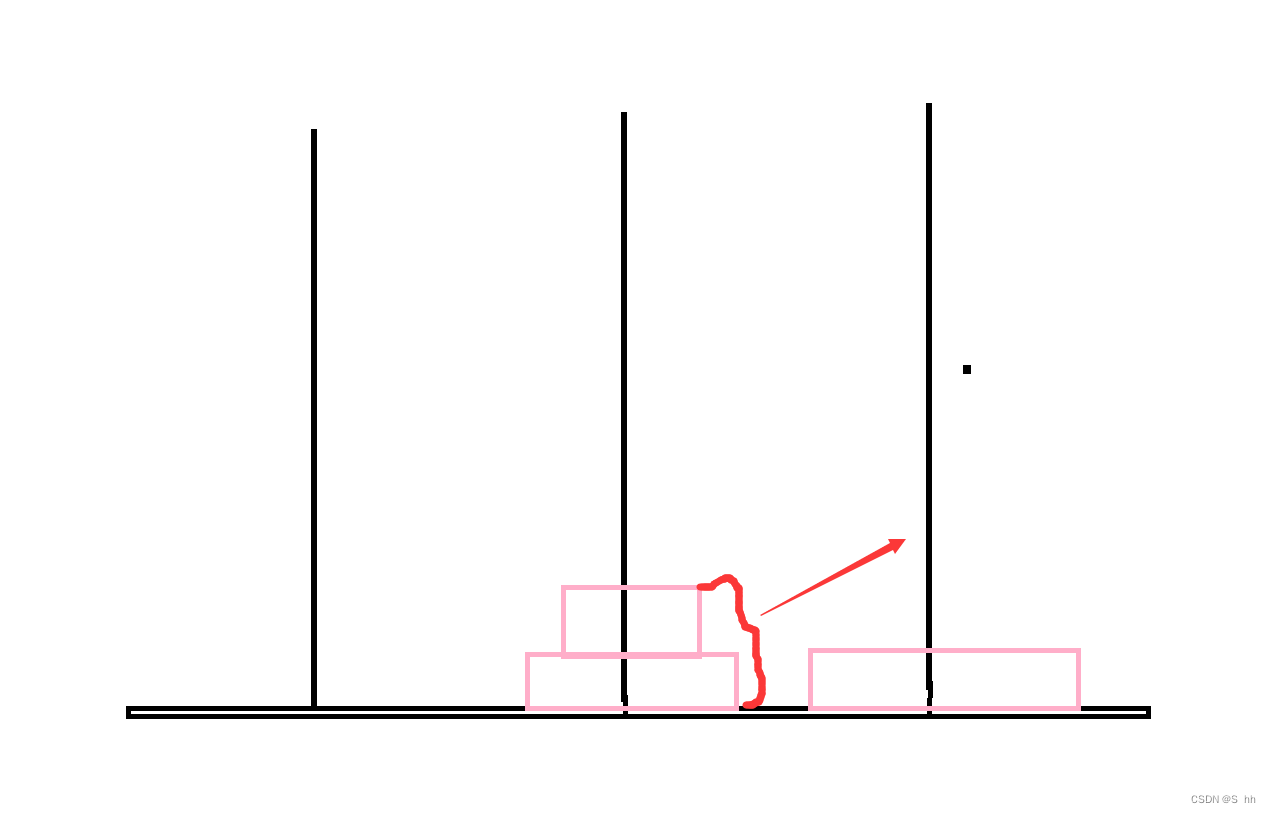
同理:
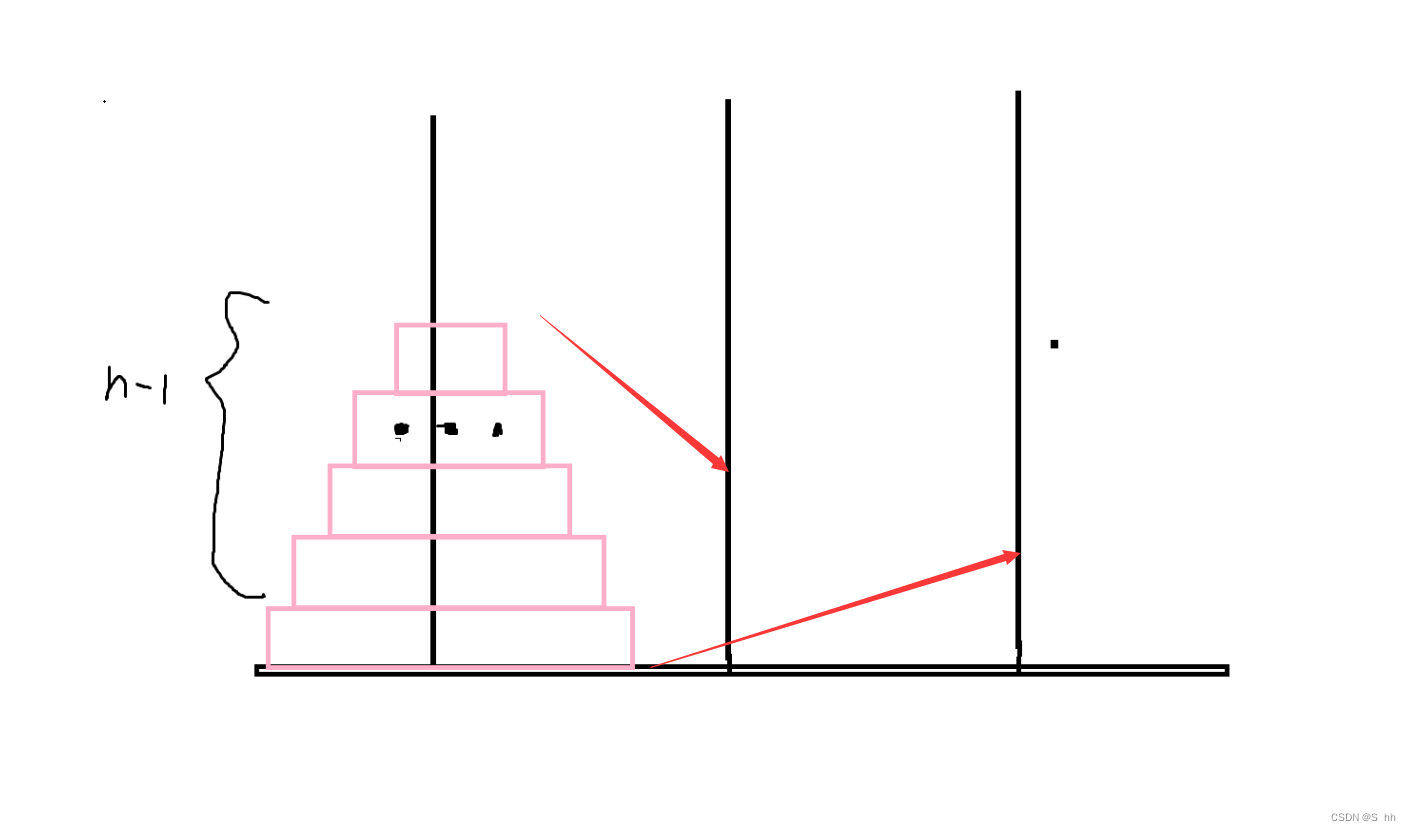
当柱子上有n个圆盘:
将n-1个圆盘移动到第二根石柱,再将最后一个移动到第三根石柱;
再将剩下的移动到第三根石柱;
Hnt(n)=2*Hnt(n-1)+1;
代码实现:
#include<stdio.h>int Hnt(int n)
{if (n == 1)return 1;return 2*Hnt(n - 1) + 1;
}
int main()
{int n;scanf("%d", &n);int t=Hnt(n);printf("%d", t);
}结语:以上就是有关函数递归的内容,希望有所帮助。

