宾馆的网站回款如何做分录网络推广网络营销外包
凸包
描述
给定n个二维平面上的点,求他们的凸包。
输入
第一行包含一个正整数n。
接下来n行,每行包含两个整数x,y,表示一个点的坐标。
输出
令所有在凸包极边上的点依次为p1,p2,...,pm(序号),其中m表示点的个数,请输出以下整数:
(p1 × p2 × ... × pm × m) mod (n + 1)
样例1输入
10
7 9
-8 -1
-3 -1
1 4
-3 9
6 -4
7 5
6 6
-6 10
0 8
样例1输出
7
样例1解释
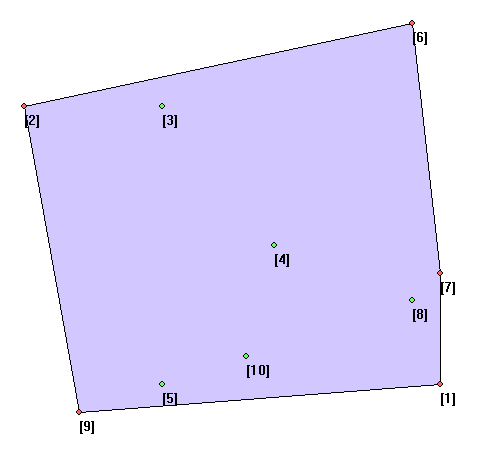
所以答案为(9 × 2 × 6 × 7 × 1 × 5) % (10 + 1) = 7
样例2
请查看下发文件内的sample2_input.txt和sample2_output.txt。
限制
3 ≤ n ≤ 10^5
所有点的坐标均为范围(-10^5, 10^5)内的整数,且没有重合点。每个点在(-10^5, 10^5) × (-10^5, 10^5)范围内均匀随机选取
极边上的所有点均被视作极点,故在输出时亦不得遗漏
时间:4 sec
空间:512 MB
代码实现
from typing import List, Tupleclass Ip:def __init__(self, x:int = 0, y:int = 0, i:int = 0) -> None:self.x = xself.y = yself.i = idef __sub__(self, other: 'Ip') -> 'Ip':return Ip(self.x - other.x, self.y - other.y)@classmethoddef read(cls, index: int) -> 'Ip':x, y = map(int, input().strip().split())return cls(x, y, index)def cross_product(a: Ip, b: Ip) -> int:return a.x * b.y - a.y * b.xdef convex(a: List[Ip]) -> List[Ip]:a.sort(key=lambda p: (p.x, p.y))b = []for p in a:while len(b) > 1:if cross_product(b[-1] - b[-2], p - b[-2]) <= 0:breakb.pop()b.append(p)temp = b[:]for p in reversed(a[:-1]):while len(b) > len(temp):if cross_product(b[-1] - b[-2], p - b[-2]) <= 0:breakb.pop()b.append(p)return b[:-1]if __name__ == "__main__":n = int(input().strip())a = [Ip.read(i + 1) for i in range(n)]b = convex(a)ans = len(b)for p in b:ans = (ans * p.i) % (n + 1)print(ans)图
描述
一个数列 a 称为合法的当且仅对于所有的位置 i, j(i < j ≤ n),都不存在一条从 aj 点连向 ai 的有向边。现在有很多个有向无环图,请你判断每个图是否只存在唯一的合法数列。
输入
输入的第一行包含一个正整数 T ,表示数据组数。
对于每组数据,第一行包含两个正整数 n, m,表示图的节点个数和边数。
接下来 m 行,每行包含两个正整数 x, y(x, y ≤ n),表示这个图有一条从 x 到 y 的有向边。
保证没有自环和重边。
输出
输出 T 行,若所给的图存在唯一的合法数列,输出 1,否则输出 0。
样例1输入
2
3 2
1 2
2 3
3 2
1 2
1 3
样例1输出
1
0
样例1解释
第一个图只有一个合法数列:1、2、3;
第二个图有两个合法数列:1、2、3 或者 1、3、2。
样例2
请查看下发文件内的sample2_input.txt和sample2_output.txt。
限制
对于50%的数据,n, m ≤ 100;
对于100%的数据,T ≤ 100, n, m ≤ 10000。
时间:4 sec
空间:512 MB
提示
[本题就是判断一个有向无环图是否存在唯一的拓扑序列。]
[回忆一下求拓扑序列是如何做的:每一次都取一个入度为0的点,将这个点取出来放进拓扑序列里,然后将这个点连向的所有点的入度减去1。]
[可以发现,在“每一次都取一个入度为0”这一步,若入度为0的点数多于1个,则显然拓扑序不唯一。]
[因此按照这个拓扑序算法做一遍就好。]
代码实现
from collections import dequedef has_unique_topological_order(n, m, edges):in_degrees = [0] * (n + 1)adj_list = [[] for _ in range(n + 1)]for x, y in edges:in_degrees[y] += 1adj_list[x].append(y)zero_degree_queue = deque()for i in range(1, n + 1):if in_degrees[i] == 0:zero_degree_queue.append(i)count = 0while zero_degree_queue:if len(zero_degree_queue) > 1:return 0node = zero_degree_queue.popleft()count += 1for neighbor in adj_list[node]:in_degrees[neighbor] -= 1if in_degrees[neighbor] == 0:zero_degree_queue.append(neighbor)return 1 if count == n else 0def main():T = int(input())for _ in range(T):n, m = map(int, input().split())edges = [tuple(map(int, input().split())) for _ in range(m)]print(has_unique_topological_order(n, m, edges))if __name__ == "__main__":main()