高端网站建设设计公司排名北京网站推广公司
目录
一、解析树
二、树的遍历
一、解析树
我们可以用解析树来表示现实世界中像句子或数学表达式这样的构造。
我们可以将((7+3)*(5-2))这样的数学表达式表示成解析树。这是完全括号表达式,乘法的优先级高于加法和减法,但因为有括号,所以在做乘法前必须先做括号内的加法和减法。树的层次性有助于理解整个表达式的计算次序。在计算顶层的乘法前,必须先计算子树中的加法和减法。
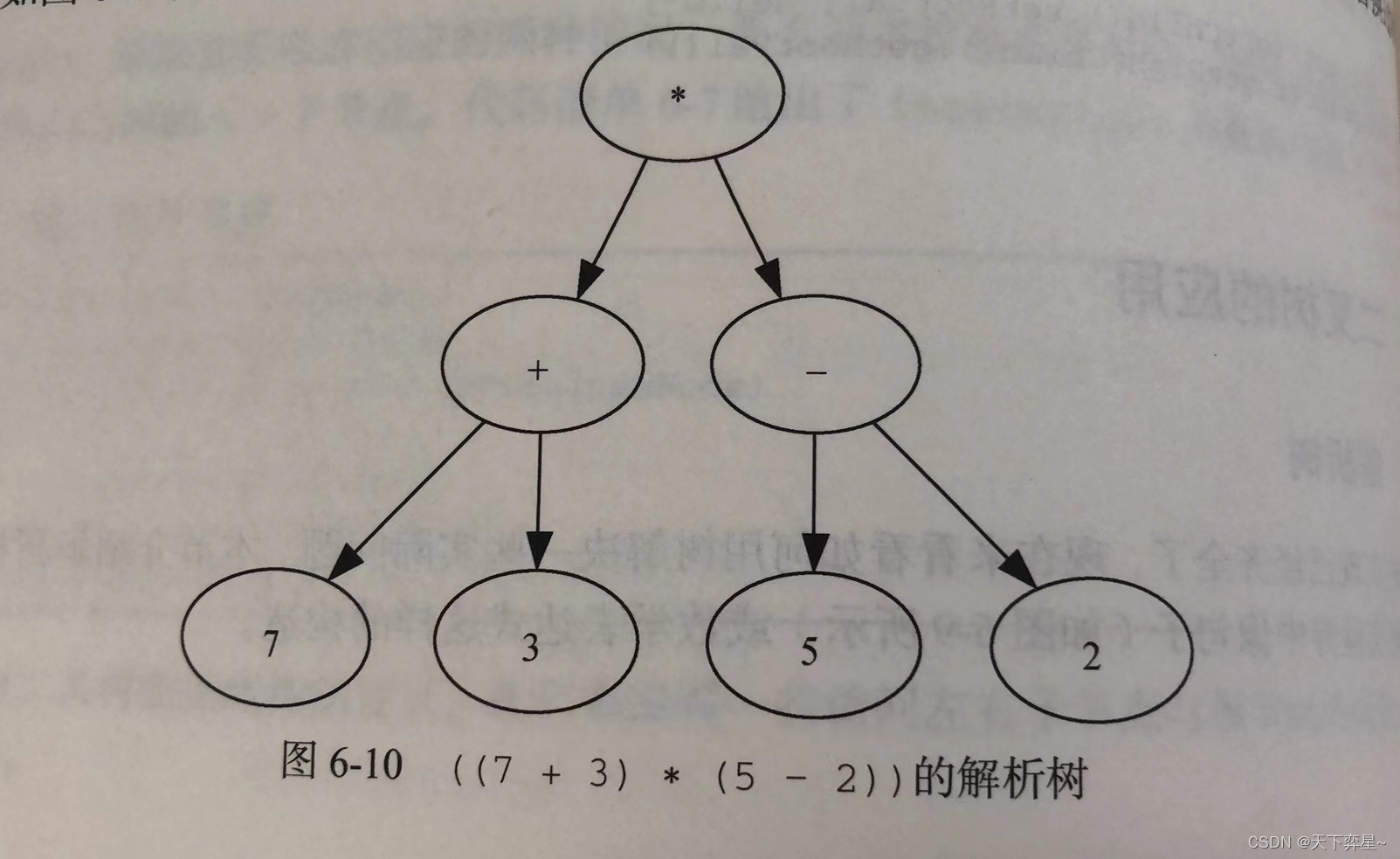
构建解析树的第一步是将表达式字符串拆分成标记列表。需要考虑4种标记:左括号、右括号、运算符和操作数。我们知道,左括号代表新表达式的起点,所以应该创建一颗对应该表达式的新树。反之,遇到右括号则意味着到达该表达式的终点。我们也知道,操作数既是叶子节点,也是其运算符的子节点。此外,每个运算符都有左右子节点。
有了上述信息,便可以定义以下4条规则:
(1)如果当前标记是(,就为当前节点添加一个左子节点,并下沉至该子节点;
(2)如果当前标记在列表['+','-','/','*']种,就将当前节点的值设为当前标记对应的运算符;为当前节点添加一个右子节点,并下沉至该子节点;
(3)如果当前标记是数字,就将当前节点的值设为这个数并返回至父节点;
(4)如果当前标记是),就跳到当前节点的父节点。
追踪父节点的方法:在遍历这棵树时使用栈记录父节点。每当要下沉至当前节点的子节点时,先将当前节点压到栈中。当要返回当前节点的父节点时,就将父节点从栈中弹出来。
解析树构建器代码如下:
from pythonds.basic import Stack
from pythonds.trees import BinaryTreedef bulidParseTree(fpexp):fplist=fpexp.split()pStack=Stack()eTree=BinaryTree('')pStack.push(eTree)currentTree=eTreefor i in fplist:if i=='(':currentTree.insertLeft('')pStack.push(currentTree)currentTree=currentTree.getLeftChild()elif i not in '+-*/)':currentTree.setRootVal(eval(i))parent=pStack.pop()currentTree=parentelif i in '+-*/':currentTree.setRootVal(i)currentTree.insertRight('')pStack.push(currentTree)currentTree=currentTree.getRightChild()elif i ==')':currentTree=pStack.pop()else:raise ValueError("Unknown Operator: "+i)return eTree计算二叉解析树的递归函数:
def evaluate(parseTree):opers={'+':operator.add,'-':operator.sub,'*':operator.mul,'/':operator.truediv}leftC=parseTree.getLeftChild()rightC=parseTree.getRightChild()if leftC and rightC:fn=opers[parseTree.getRootVal()]return fn(evaluate(leftC),evaluate(rightC))else:return parseTree.getRootVal()二、树的遍历
我们将对所有节点的的访问称为“遍历”,共有3种遍历方式,分别为前序遍历、中序遍历和后序遍历。
前序遍历:
在前序遍历中,先访问根节点,然后递归地前序遍历左子树,最后递归地前序遍历右子树。
中序遍历:
在中序遍历中,先递归地中序遍历左子树,然后访问根节点,最后递归地中序遍历右子树。
后序遍历:
在后序遍历中,先递归地后序遍历左子树,然后递归地后序遍历右子树,最后访问根节点。
遍历树的代码格外简洁,这主要是因为遍历是递归的。
将前序遍历算法实现为外部函数:
def preorder(tree):if tree:print(tree.getRootVal())preorder(tree.getLeftChild())preorder(tree.getRightChild())将前序遍历算法实现为BinaryTree类的方法:
def preorder(self):print(self.key)if self.leftChild:self.left.preorder()if self.rightChild:self.right.preorder()后序遍历函数:
def postorder(tree):if tree!=None:postorder(tree.getLeftChild())postorder(tree.getRightChild())print(tree.getRootVal())后序求值函数:
def postordereval(tree):opers={'+':operator.add,'-':operator.sub,'*':operator.mul,'/':operator.truediv}res1=Noneres2=Noneif tree:res1=postordereval(tree.getLeftChild())res2=postordereval(tree.getRightChild())if res1 and res2:return opers[tree.getRootVal()](res1,res2)else:return tree.getRootVal()中序遍历函数:
def inorder(tree):if tree!=None:inorder(tree.getLeftChild())print(tree.getRootVal())inorder(tree.getRightChild())修改后的中序遍历函数,它能还原完全括号表达式:
def printexp(tree):sVal=""if tree:sVal='('+printexp(tree.getLeftChild())sVal=sVal+str(tree.getRootVal())sVal=sVal+printexp(tree.getRightChild())+')'return sVal